Å løyse andregradslikningar med abc-formelen
Vi ser på den generelle andregradslikninga . Her får vi eit lite problem ved at dei same bokstavane og er brukte både til å illustrere kvadratsetninga og andregradsuttrykket. Vi løyser dette ved å bruke bokstavane og i kvadratsetninga slik at denne blir
Det er godt mogleg at du kan komme fram til abc-formelen på eiga hand. Prøv deg utan å sjå på løysinga.
Tips: Bruk metoden med å danne fullstendig kvadrat.
Utleiing av abc-formelen
abc-formelen
Andregradslikninga
Vi bruker teiknet
Når vi løyser ei andregradslikning med abc-formelen, ordnar vi først likninga slik at ho kjem på forma
Du hugsar kanskje at vi definerte kvadratrota berre til positive tal og null? Det vil seie at andregradslikninga ikkje har løysingar mellom dei reelle tala når det som står under rotteiknet, er mindre enn null. Kanskje det digitale verktøyet du bruker, då gir løysingar med bokstaven
Andregradslikninga har berre éi løysing når det som står under rotteiknet, er lik null.
Vi skal no sjå på nokre døme på bruk av abc-formelen.
Døme 1
Likninga har to løysingar. Det er altså to verdiar for
Døme 2
Uttrykket under rotteiknet er null, og vi får berre éi løysing.
Døme 3
Vi får
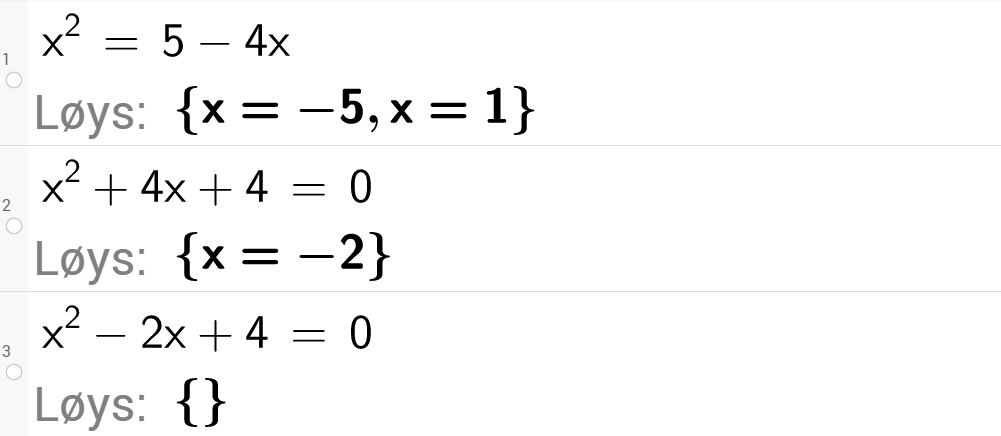
Ved CAS i GeoGebra får vi løysingane nedanfor ved å bruke knappen
Legg merke til markeringa for "inga løysing" i linje 3.