Definisjon av vektor

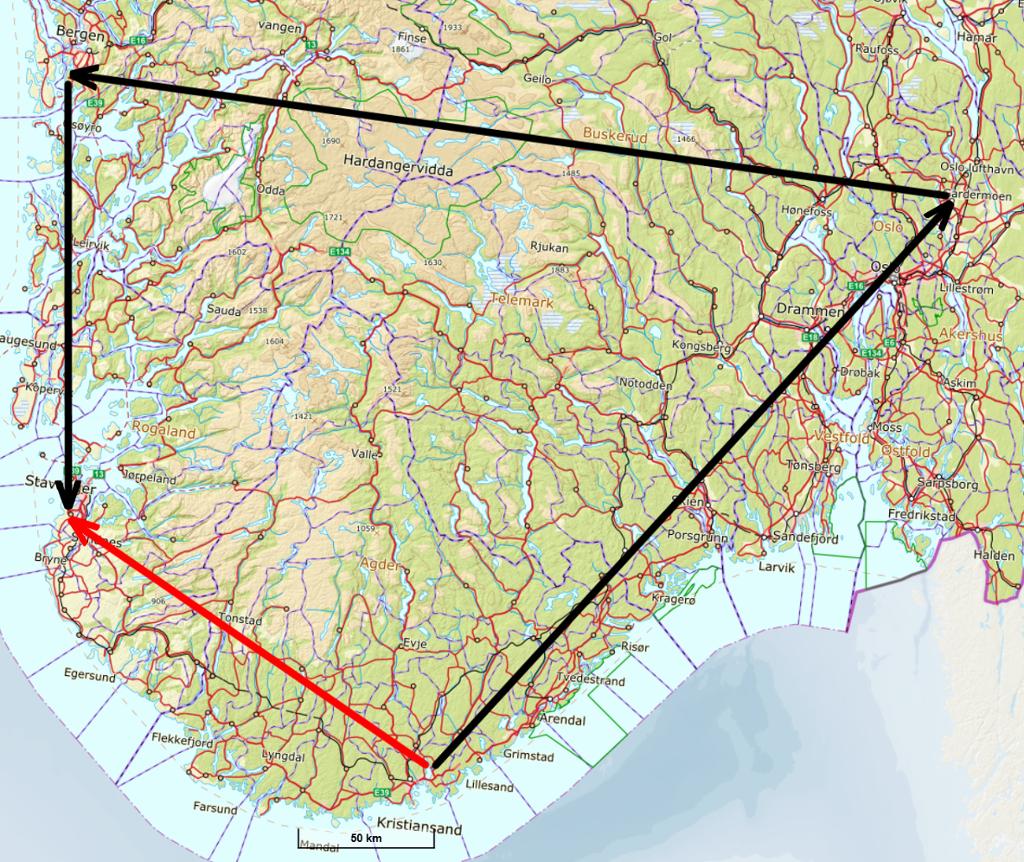
Tenk deg en flyreise som starter i Kristiansand, går via Oslo og Bergen og ender i Stavanger. Reisen kan illustreres med piler som vist på kartet.

Pilene illustrerer de aktuelle forflytningene. Lengdene på pilene forteller om lengdene på flyreisene, og retningene på pilene forteller om retningene på reisene.

Hvis formålet med flyreisene var å forflytte seg fra Kristiansand til Stavanger, kunne alle flyreisene vært erstattet av en eneste flyreise, nemlig direkte fra Kristiansand til Stavanger. Den røde pila viser denne reisen, som vi kan si er "sluttresultatet" eller "summen" av alle reisene.

Forflytning er et eksempel på en størrelse der vi må kjenne til både lengden og retningen for å beskrive størrelsen fullstendig. Fra naturfag (fysikk) kjenner du begrepene kraft, fart og akselerasjon. Dette er også størrelser med retning. Det har vist seg svært hensiktsmessig å tegne disse størrelsene som piler. Slike størrelser som har både lengde og retning, kaller vi vektorer, og størrelsene kaller vi vektorstørrelser eller bare vektorer.

En størrelse som ikke har retning, kalles en skalar. Et pengebeløp er et eksempel på en skalar.

Når vi skal gi vektorer navn, bruker vi bokstaver med ei pil over. Det er vanlig å bruke små bokstaver, som figuren viser.

Når en vektor går fra et punkt til et annet, bruker vi store bokstaver. Vektoren mellom to punkter $A$ og $B$ får navnet $$ \overrightarrow{AB}$$. Vi sier at denne vektoren har utgangspunkt i $A$ og endepunkt i $B$. Hva er forskjellen på $\overrightarrow{AB}$ og $\overrightarrow{BA}$?

En vektor har altså både lengde og retning. La $$ \overrightarrow{s}$$ være forflytning 3 kilometer vestover. Vi sier at lengden av vektoren er 3 kilometer, og at retningen er vestover. Når vi skal beskrive en vektor, er det viktig å skille klart mellom disse to egenskapene.

Fra før vet du kanskje hva vi mener med absoluttverdien til et tall. Vi kan se på det som lengden på tallet eller avstanden fra 0 til tallet. Vi noterer det slik:

$\left|t\right|$ er absoluttverdien til tallet $t$.

$$ \begin{array}{rcl}\left|t\right| & =& t \mathrm{hvis} t\ge 0.\\ & & \\ \left|t\right| & =& -t \mathrm{hvis} t<0.\end{array}$$

Absoluttverditegn brukes også for å angi lengden av en vektor. Vi skriver at:

$$ \left|\overrightarrow{s}\right|=3 \mathrm{km}$$

Lengden av en vektor er altså en skalar, mens vektoren selv er bestemt ved både en lengde og en retning.

Hvis du kan parallellforskyve en vektor slik at den dekker en annen vektor, er de to vektorene like.

Dette betyr for eksempel at hvis vi flytter den røde vektoren som går fra Kristiansand til Stavanger slik at den starter i Oslo og går i nord-vestlig retning til områdene rundt Hemsedal, vil vi ha den samme vektoren selv om den er tegnet et annet sted i kartet.