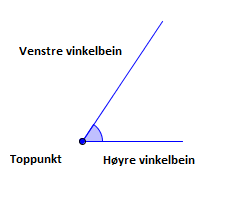
Vinkler
Når to stråler har felles endepunkt, danner de en vinkel. Det felles endepunktet kalles for vinkelens toppunkt. Strålene kalles for vinkelbein.
Sett fra toppunktet får vi høyre vinkelbein og venstre vinkelbein.
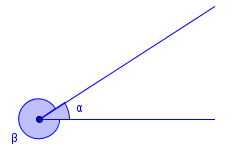
To stråler med felles endepunkt danner egentlig to vinkler. Se figuren. Når vi snakker om vinkelen mellom to stråler, mener vi vanligvis den minste vinkelen, på figuren.
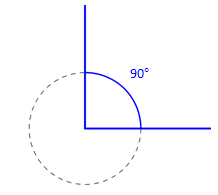
Det er vanlig å dele sirkelens omkrets i 360 deler, eller grader. Måling av vinkler bygger på denne inndelingen.
Vi tenker oss at vi plasserer en sirkel med sentrum i toppunktet til en vinkel.
En vinkel som spenner over en fjerdedel av sirkelens omkrets er da . Denne vinkelen kaller vi en rett vinkel.
En vinkel som spenner over halvparten av sirkelens omkrets er 180°.
En vinkel mellom 0° og 90° kaller vi en spiss vinkel.
En vinkel mellom 90° og 180° kaller vi en stump vinkel.
To vinkler som til sammen er 90° kaller vi komplementvinkler.
To vinkler som til sammen er 180° kaller vi supplementvinkler.
To linjer som danner en vinkel på 90 grader med hverandre, sier vi står normalt på hverandre.
Vi skriver .
Nå to linjer skjærer hverandre, er to og to av de fire vinklene som dannes alltid like store.
På figuren er og supplementvinkler. Det betyr at
Vi har også at
Det må bety at .
Samme resonnement gir at .
Vinklene og kaller vi toppvinkler. Det samme gjelder og . Toppvinklene er alltid like store.
En linje skjærer to andre linjer, og . Av de vinklene som dannes, er to vinkler med forskjellig toppunkt samsvarende hvis overskjæringslinjen utgjør enten høyre vinkelbein i begge vinklene eller venstre vinkelbein i begge vinklene.
På figuren er (alfa) og (beta) et par av samsvarende vinkler, og (gamma) og (delta) er et annet par av samsvarende vinkler. Overskjæringslinjen er venstre vinkelbein i alle vinklene.
På figuren er og samsvarende vinkler fordi venstre vinkelbein er felles
(linjen ).
I tillegg er høyre vinkelbein, linjene og parallelle. Tenk deg at du roterer figuren 180° om midtpunktet mellom de to skjæringspunktene.
Ser du at ?
Når to parallelle linjer skjæres av en tredje linje, er de samsvarende vinklene like store.
Og motsatt, dersom samsvarende vinkler er like store, er de overskårne linjene parallelle.

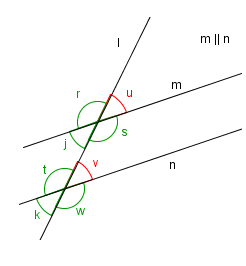
Hvor store er vinklene og sammenliknet med og når ? Prøv å begrunne svarene dine.
At summen av vinklene i en trekant alltid er lik 180° kombinert med setningen som sier at toppvinkler er like store, gir følgende nyttige setning
Når vinkelbeina til to vinkler, og , står parvis normalt på hverandre, er .
Bruk figuren til å forklare hvorfor dette er riktig.