Hvordan bestemme den deriverte i et punkt numerisk
Til nå har vi sett på hvordan vi kan finne den deriverte eksakt, enten algebraisk som grenseverdien til et uttrykk eller grafisk som stigningstallet til en tangent. I dette avsnittet skal vi finne den deriverte i et punkt numerisk, men for å gjøre det må vi vite hva det vil si å løse noe numerisk.
Du har kanskje lagt merke til at det for eksempel i GeoGebra er to alternativer for å løse en likning, markert med eller
Det å finne et tall numerisk skiller seg fra andre måter å regne på ved at det er en form for såkalt prøve-og-feile-metode. Det vil si at man starter med et forslag til løsning, og ved hjelp av ulike mønstre nærmer man seg den egentlige løsningen. Når GeoGebra har funnet en løsning, slutter programmet å lete, selv om det kan finnes flere løsninger. Dette er en viktig grunn til alltid å velge eksakt løsning av likninger, for så å runde av svarene etterpå.
Vi kan se et eksempel under der vi forsøker å løse et likningssett:
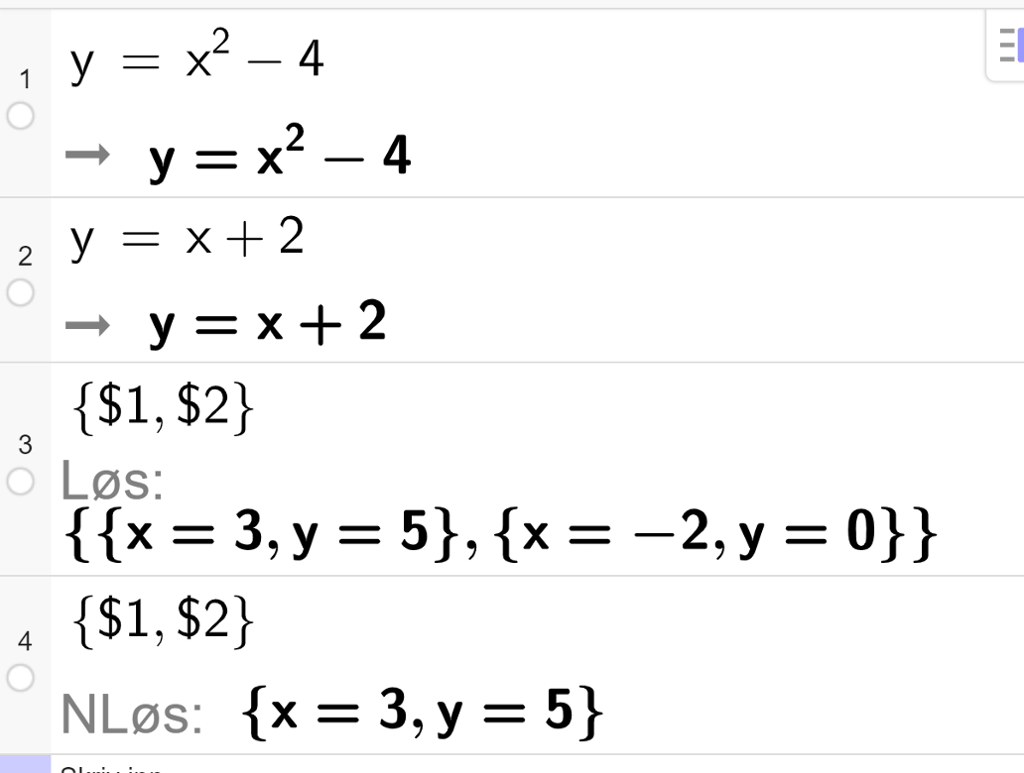
I 1T brukte vi numeriske metoder både for hånd og ved hjelp av programmering. Vi fant blant annet nullpunkt gjennom halveringsmetoden og tilnærmede verdier for den deriverte med programmering. Du finner lenker til de to sidene lengst ned på denne sida. Å lete etter løsninger slik vi har gjort tidligere, er tidkrevende hvis man skal gjøre det for hånd, så dette er en oppgave for datamaskiner.
Vi skal her vise en annen måte vi kan bruke når vi skal finne en tilnærming til den deriverte gjennom programmering. Vi skal ta utgangspunkt i formelen for stigningstallet til ei rett linje for å finne stigningstallet til tangenten. Vi minner om den generelle formelen for stigningstall:
Vi tar for oss funksjonen
Vi plasserer punkter med lik avstand til punktet
Vi må bestemme oss for hvor nært vi skal komme før vi sier oss fornøyd. Vi kan for eksempel bestemme at vi skal slutte å gå nærmere hvis forskjellen mellom to påfølgende tilnærminger er mindre enn 0,000 1.
Vi velger å starte med at avstanden mellom punktene er 1, og så halverer vi avstanden helt til vi har nådd målet. Bildet viser startpunktet for programmet med tangenten og de to sekantene tegnet inn med sine stigningstall:
La oss rydde i opplysningene over i en algoritme:
Først definerer vi funksjonen.
Vi definerer
x Vi setter startverdien for avstand fra
B C A Vi setter nøyaktigheten for tilnærmingen til
h Vi setter startverdien for den deriverte til
tangent.Vi setter startverdien til forskjellen mellom to påfølgende tilnærminger til
h + 1 Vi starter ei løkke som skal gå så lenge forskjellen mellom to påfølgende tilnærminger er større enn
h Vi regner ut stigningstallene til de to sekantene.
Vi regner ut gjennomsnittet av stigningstallet til de to sekantene.
Vi regner ut forskjellen mellom de to sekantene.
Vi legger den siste tilnærmingen inn i variabelen
tangent.Vi halverer avstanden og starter løkka på nytt.
Vi må skrive ut tilnærmingen når vi har kommet langt nok.
Da kan vi få et program som ser slik ut:
1def f(x): 2 return x**3+4*x**2-x 3 4x = 1 #punktet vi skal finne den deriverte i 5avstand = 1 #hvor langt vi skal gå til hver side 6h = 0.0001 #hvor nøyaktig vi krever at tilnærmingen skal være 7 8 9tangent = 20 #startverdi for den deriverte 10 11forskjell = h+1 #startverdi for while-løkka 12 13 14while abs(forskjell) > h: #vilkåret for løkka er at forskjellen mellom 15 #denne og forrige tilnærming er større enn h 16 sek_v = (f(x)-f(x-avstand))/avstand #stigningstallet til venstre sekant 17 sek_h = (f(x+avstand)-f(x))/avstand #stigningstallet til høyre sekant 18 tangent_2 = (sek_v + sek_h)/2 #gjennomsnittet til de to stigningstallene 19 forskjell = tangent_2 - tangent #forskjellen mellom denne og forrige tilnærming 20 tangent = tangent_2 #legger den siste tilnærmingen inn i 21 #plassholderen "tangent" 22 avstand = avstand/2 #halverer avstanden til punktet x = 1 23 24print(f"Den deriverte i {x} er tilnærmet lik {tangent:.4f}.") 25
Related content
Her bruker vi halveringsmetoden til å finne en tilnærmet verdi for ett av nullpunktene til en funksjon.
Her skal du lage et program som kan regne ut tilnærmede verdier for den deriverte – som er det samme som tilnærmede verdier for momentan vekstfart.