Konvergens og divergens i uendelige geometriske rekker
1.1.40
Undersøk om de geometriske rekkene under konvergerer eller divergerer. Dersom de konvergerer: Finn summen de konvergerer mot.
a)
Løsning
Vi finner
Siden vi har at
b)
Løsning
Vi leser her ut av formelen at
c)
Løsning
Her leser vi ut fra formelen at
d)
Løsning
Vi observerer at dette er den samme rekka som i b), altså konvergerer den, og summen er 6.
e)
Løsning
Vi har her ei geometrisk rekke med
Dette er den samme rekka som i a), og summen er dermed
f)
Løsning
Vi skriver om uttrykket for
Vi ser at vi har ei geometrisk rekke med
Vi har at
Vi finner summen:
Her kan vi også legge merke til at dette er det samme som rekka i e) multiplisert med
g)
Løsning
Vi finner
Vi har at
h)
Løsning
Vi skriver om uttrykket for
Vi har dermed at
1.1.41
Finn konvergensområdet til rekkene, og finn et uttrykk for summen i hvert tilfelle.
a)
Løsning
Vi finner først
Vi må ha at
Summen av rekka blir da
b)
Løsning
Vi finner først
Dette gir det samme konvergensområdet som i a), altså
c)
Løsning
Vi må løse dobbeltulikheten
Vi deler dobbeltulikheten i to og løser de to enkle ulikhetene hver for seg.
Venstre ulikhet:
Vi har to kritiske punkter,
Vi har at venstre ulikhet har løsningen
Høyre ulikhet:
Vi har to kritiske punkter,
Vi har at høyre ulikhet har løsningen
Vi må finne det området som oppfyller begge ulikhetene samtidig. Vi tegner en figur for å få oversikt:
Dette gir oss konvergensområdet:
Vi finner et uttrykk for summen:
I GeoGebra kan vi løse hele denne oppgaven med noen få tastetrykk:
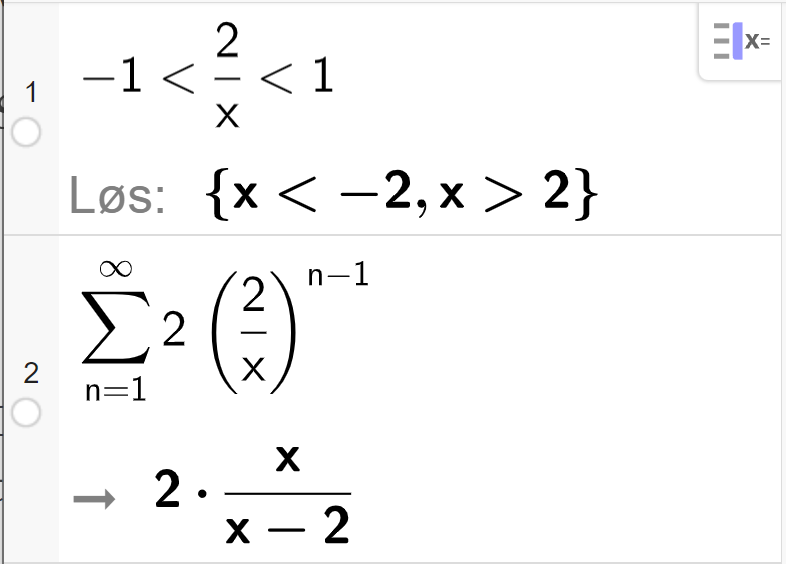
d)
Løsning
Vi starter med å finne
Vi løser dobbeltulikheten:
Vi har altså at
Vi leser ut av formelen at
e)
Løsning
Vi leser ut av formelen at
Vi deler opp i to ulikheter:
Vi har at konvergensområdet er
For å finne
1.1.42
Ta for deg rekkene i oppgave 1.1.41, og finn ut om summen av hver rekke kan bli 1 eller 4. Oppgi også hva
Løsning a)
For hånd:
Vi setter formelen vi fant for summen lik 1:
Vi ser at vi får summen lik 1 dersom vi setter
Vi gjør det samme med 4:
Vi ser at vi får summen lik 4 dersom vi setter
Når det gjelder løsning i CAS, kan vi enten bruke formelen for summen vi fant i 1.1.41 slik vi gjorde for hånd, eller vi kan bruke den eksplisitte formelen for
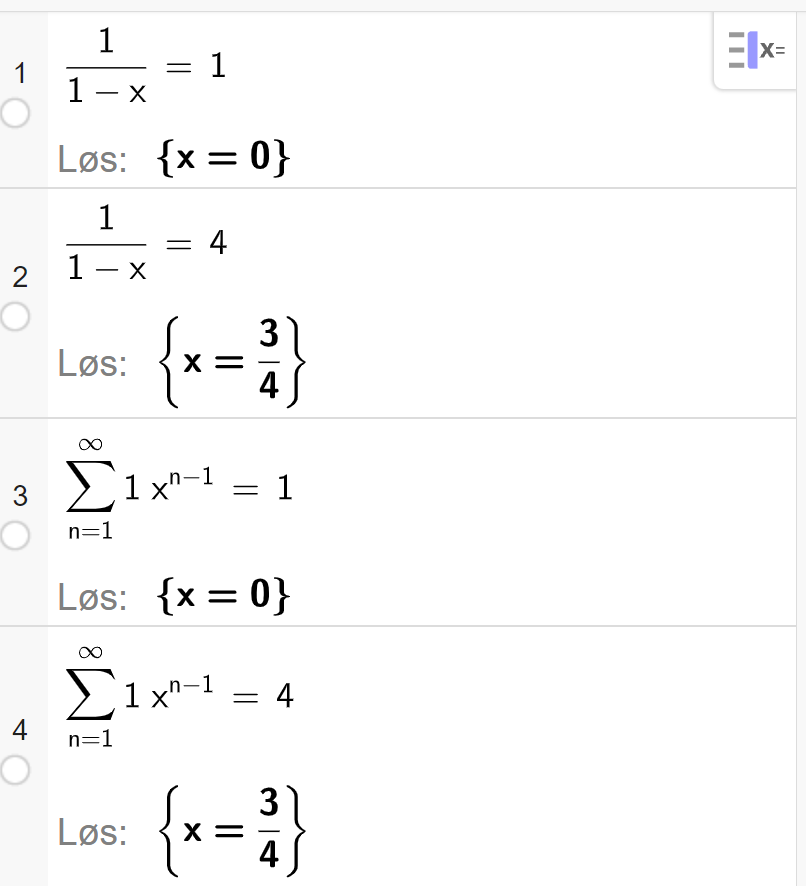
Løsning b)
For hånd:
Her ser vi at vi ikke har noen løsning på likningen, altså kan ikke summen bli 1.
Her finner vi en løsning på likningen, men vi ser at den ligger utenfor konvergensområdet, og derfor kan summen heller ikke bli 4.
Vi løser i CAS, her viser vi bare løsningen med summeformel:
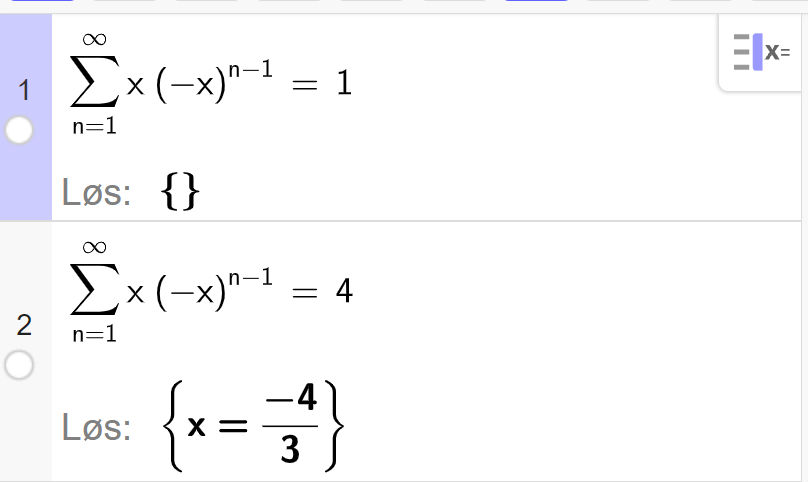
Legg merke til at GeoGebra gir deg et svar på likningen selv om denne summen ikke finnes! Antageligvis finner GeoGebra formelen for summen først, slik vi har gjort, og løser likningen med den uten å kunne ta med seg konvergensintervallet.
Løsning c)
I resten av disse oppgavene viser vi kun løsning for hånd. Se på de to foregående oppgavene hvis du ikke husker hvordan du skal løse i CAS.
Vi ser at
Denne løsningen er innenfor konvergensintervallet. Det betyr at summen
Løsning d)
Denne løsningen er innenfor konvergensintervallet, så summen blir 1 når
Denne løsningen er også innenfor konvergensintervallet, så summen blir 4 når
Løsning e)
Vi ser at begge løsningene ligger innenfor konvergensområdet, og vi har at
1.1.43
Ta for deg rekkene i oppgave 1.1.41 a) og c). Avgjør hva som er den største og den minste summen rekka kan konvergere mot.
Løsning a)
Vi har at summen av rekka er gitt ved
Vi deriverer funksjonen i CAS:
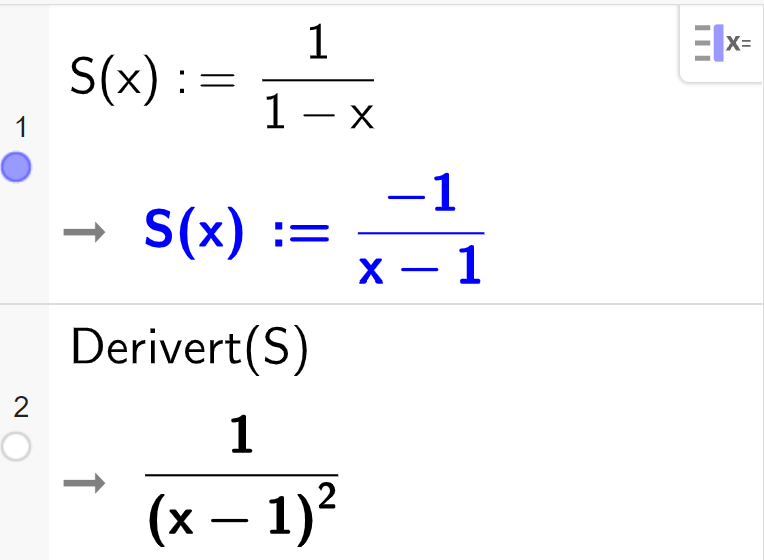
Vi legger merke til at den deriverte alltid er positiv. Det vil si at funksjonen er strengt voksende i hele konvergensintervallet. Vi kan ikke finne en bestemt høyeste verdi og laveste verdi fordi summen ikke er definert i ytterpunktene i intervallet, men vi kan finne grenseverdiene til summen.
Den laveste verdien finner vi ved å la
Den høyeste verdien finner vi ved å la
Vi ser at vi får 0 i nevneren, men ikke i telleren. Det vil si at uttrykket ikke har noen grenseverdi, men vil gå mot uendelig.
Vi ser at nedre grenseverdi for summen av rekka er
Det kan være lurt (men ikke nødvendig!) å kikke på grafen til funksjonen for å få bedre oversikt:
Vi ser at det vi fant ved regning, stemmer bra med bildet av grafen.
Løsning c)
Vi har at summen er gitt ved
Igjen starter vi med å derivere for å undersøke monotoniegenskapene til funksjonen:
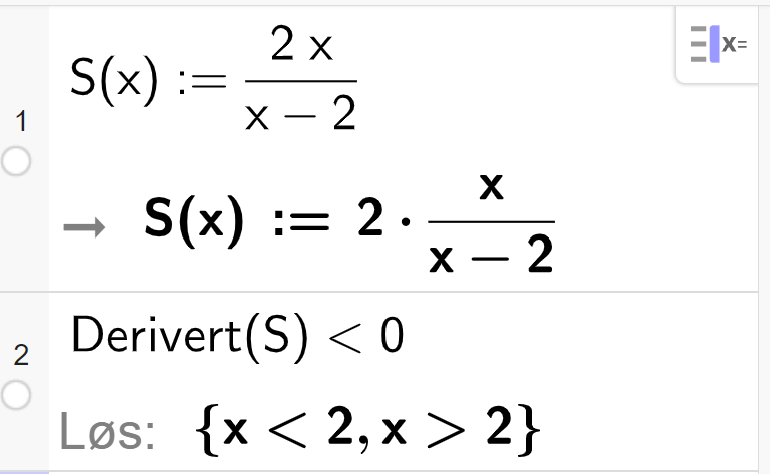
Vi legger merke til at den deriverte er negativ i hele konvergensområdet, det vil si at vi må lete etter den høyeste verdien der
Vi finner disse grenseverdiene:
Vi har altså at den nedre grenseverdien til summen av rekka er 1, og det eksisterer ikke en øvre grenseverdi. Vi legger også merke til at summen ikke kan bli 2.
Et tips er også her å tegne grafen hvis du vil ha bedre oversikt.