Bargobihttá

Fakultet, Pascals talltrekant og binomialformelen

Her kan du bli bedre kjent med fakultet, Pascals talltrekant og binomialformelen.

4.2.20

På hvor mange måter kan vi sortere

a) åtte biler

Løsning

8! = 40320

b) 11 kosedyr

Løsning

11! = 39 916 800

c) 34 tall

Løsning

$34! \approx 2, 9 \cdot 10^{38}$

4.2.21

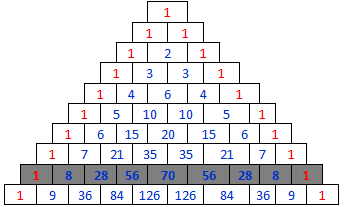
a) Skriv opp Pascals talltrekant til og med rad nummer 9 (husk at vi begynner å telle på 0).

Løsning

Pascals talltrekant. Den første raden inneholder tallet 1. Den neste raden inneholder to ettall. Antall tall øker med 1 for hver rad nedover. Det første og siste tallet i en rad er alltid 1. Et tall inne i trekanten er lik summen av de to nærmeste tallene i raden over. Illustrasjon. — Govva: Grete Larsen / CC BY-NC-SA 4.0

b) Bruk talltrekanten du skrev opp til å finne ut på hvor mange måter du kan trekke ut 5 basketspillere fra en stall på 8.

Løsning

Vi går inn i rad nummer 8 på talltrekanten og finner plass nummer 5. Vi finner at det er 56 måter å trekke ut 5 spillere på.

c) Skriv opp rad nummer 12 i Pascals talltrekant med binomialkoeffisienter.

Løsning

$(\begin{matrix} 12 \\ 0 \end{matrix}) (\begin{matrix} 12 \\ 1 \end{matrix}) (\begin{matrix} 12 \\ 2 \end{matrix}) (\begin{matrix} 12 \\ 3 \end{matrix}) (\begin{matrix} 12 \\ 4 \end{matrix}) (\begin{matrix} 12 \\ 5 \end{matrix}) (\begin{matrix} 12 \\ 6 \end{matrix}) (\begin{matrix} 12 \\ 7 \end{matrix}) (\begin{matrix} 12 \\ 8 \end{matrix}) (\begin{matrix} 12 \\ 9 \end{matrix}) (\begin{matrix} 12 \\ 10 \end{matrix}) (\begin{matrix} 12 \\ 11 \end{matrix}) (\begin{matrix} 12 \\ 12 \end{matrix})$

4.2.22

I en hatt ligger det seks kuler. Bruk Pascals talltrekant og svar på oppgavene:

a) På hvor mange måter kan du trekke ut éi kule fra hatten?

b) På hvor mange måter kan du trekke ut to kuler fra hatten?

c) På hvor mange måter kan du trekke ut tre kuler fra hatten?

d) På hvor mange måter kan du trekke ut fire kuler fra hatten?

e) På hvor mange måter kan du trekke ut fem kuler fra hatten?

f) På hvor mange måter kan du trekke ut seks kuler fra hatten?

Løsning

Vi bruker talltrekanten vi tegnet i 4.2.21 a) og går inn i linje nummer 6. Vi hopper over plass nummer 0 og finner løsningene våre fra og med plass nummer 1:

a) 6, b) 15, c) 20, d) 15, e) 6, f) 1

4.2.23

Finn svaret på alle deloppgavene i 4.2.20

a) ved å bruke GeoGebra

b) ved å lage et dataprogram

4.2.24

Finn ut på hvor mange ulike måter det kan velges ut ei gruppe på 8 personer

a) fra klassen din

b) fra trinnet ditt

c) fra skolen din

d) fra byen din

4.2.20

4.2.21

4.2.22

4.2.23

4.2.24

Njuolggadusat teavstta geavaheapmái "Fakultet, Pascals talltrekant og binomialformelen"