Definisjonen av den deriverte
Fagstoff
Fagartikkel
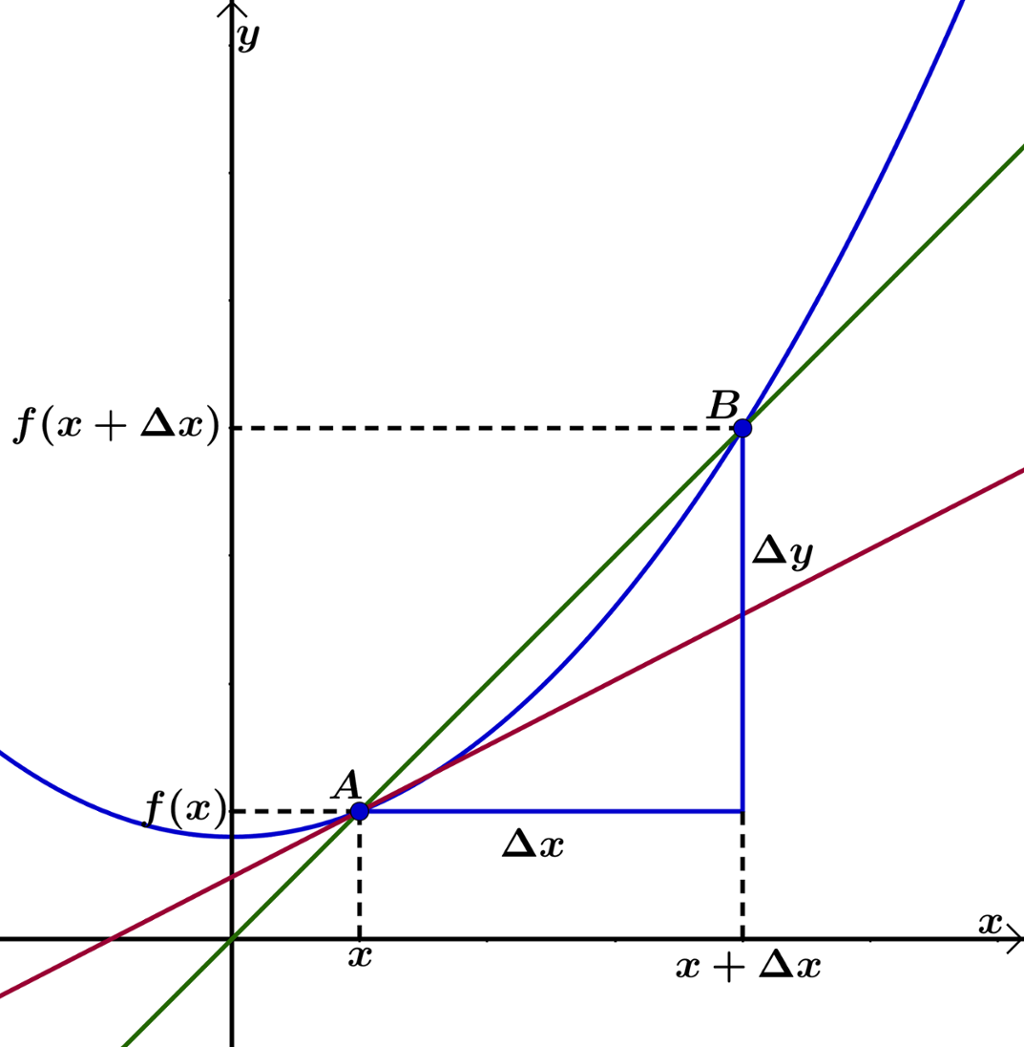
Her ser vi korleis vi kan finne den deriverte til ein funksjon ved manuell rekning, og vi definerer den deriverte funksjonen.
Opne i fag:
Her ser vi korleis vi kan finne den deriverte til ein funksjon ved manuell rekning, og vi definerer den deriverte funksjonen.
