Bruk av formlikskap for å rekne ut ukjende sider i trekantar
Trekantane og er formlike. Rekn ut lengdene av dei ukjende sidene.
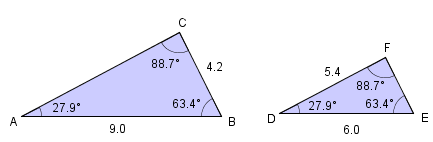
Her ser vi at sidene og er tilsvarande sider fordi begge er motståande sider til vinklane på . Sidene og ligg begge motsatt av vinklane som er og er også tilsvarande. Det same er sidene og .
Vi kan finne dei ukjende sidene ved å bruke målestokken.
Vi reknar ut målestokken når vi går frå til . Målestokken er
Det tyder at
.
Når vi går motsett veg, må vi dele med målestokken. Det tyder at
Eit tre står på ei horisontal slette. Vi skal finne ut kor høgt treet er utan å felle det.
Utstyr: Sol og metermål
Vi set ein pinne ned i bakken litt bortanfor treet og måler avstanden skyggen kastar ved pinnen og ved treet. Sjå figuren nedanfor.
Både pinnen og treet dannar ein vinkel på med bakken, og solstrålane dannar same vinkel med bakken der pinnen står som der treet står. Vi får difor to formlike trekantar, og det går fram av figuren kva for sider som er tilsvarande.
Vi reknar ut målestokken når vi går frå den minste trekanten til den største trekanten
Legg merke til at vi òg kan finne den ukjende sida ved å bruke likning.
Vi set høgda av treet lik , og sidan forholdet mellom tilsvarande sider er konstant, kan vi setje opp og løyse likninga
Treet er meter høgt.
Spørsmål
Løysingsmetoden vår set krav til terrenget der treet står. Kva for krav er det?
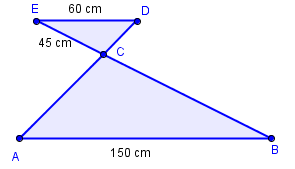
På figuren er og parallelle. Linjestykkene og skjer kvarandre i .
Oppgåve
Vis at og er formlike, og bruk dette til å rekne ut lengda av sida .
Løysing
sidan desse er toppvinklar. Då er sidene og tilsvarande sider.
fordi venstre vinkelbein er felles og høgre vinkelbein er parallelle i dei to vinklane. (Samsvarande vinklar ved parallelle vinkelbein).
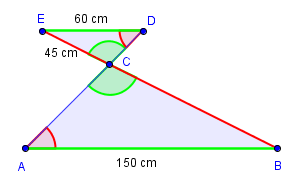
Sidene og er då tilsvarande sider fordi dei er motståande sider til like store vinklar.
Vinklane i dei to trekantane er parvis like store, og trekantane er formlike.
Vi reknar ut målestokken når vi går frå den minste trekanten til den største.
Då er
Også her kan vi løyse oppgåva ved å setje opp og løyse ei likning sidan forholdet mellom tilsvarande sider er konstant. Det er lurt å alltid byrje med den ukjende sida.
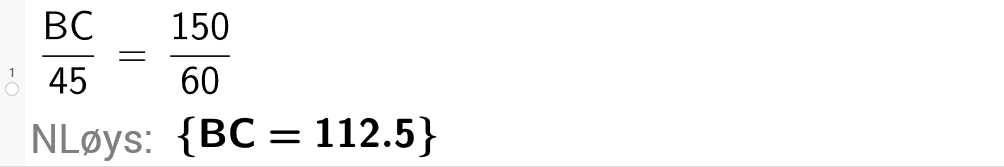
Likninga kan vi også løyse med CAS i GeoGebra, sjå figuren.