Ulikskapar av tredje grad

Vi skal løyse ulikskapen

$-4x^2<x-4-x^3$

Vi ordnar ulikskapen slik at vi får null på høgre side. Då kan vi faktorisere venstresida, og ulikskapen kan løysast ved å studere forteiknet til det faktoriserte uttrykket.

$x^3-4x^2-x+4<0$

Her har vi ikkje nokon informasjon som kan gje oss den første løysinga av likninga $x^3-4x^2-x+4=0$. Difor må vi prøve oss fram, og vi finn at uttrykket $x^3-4x^2-x+4$ blir null for $x=1$.

$1^3-4·1^2-1+4=1-4-1+4=0$

Det viser at $\left(x-1\right)$ er ein faktor i $x^3-4x^2-x+4$.

Vi utfører så polynomdivisjonen

$\begin{array}{ccccccccccccccccccc}& x^3& -& 4& x^2& -& & x& +& 4& )& :& (& x& -& 1& )& =& x^2-3x-4 \\ -(& x^3& -& & x^2& )& & & & & & & & & & & & & \\ & & -& 3& x^2& -& & x& & & & & & & & & & & \\ -& (& -& 3& x^2& +& 3& x& )& & & & & & & & & & \\ & & & & & -& 4& x& +& 4& & & & & & & & & \\ & & & -& (& -& 4& x& +& 4& )& & & & & & & & \\ & & & & & & & & & 0& & & & & & & & & \end{array}$

Vi set $x^2-3x-4=0$ og finn nullpunkta

$\begin{array}{rcl}{x}^2-3x-4& = & 0\\ & & \\ x& =& \frac{-\left(-3\right)\pm \sqrt{{\left(-3\right)}^2-4·1·\left(-4\right)}}{2·1}\\ & & \\ x& =& \frac{3\pm 5}{2}\\ & & \\ x_1& =& 4 , x_2=-1\\ & & \end{array}$

Vi har dermed nullpunkta $x=-1$, $x=1$ og $x=4$.

Det tyder at

$x^3-4x^2-x+4=\left(x+1\right)\left(x-1\right)\left(x-4\right)$

Ulikheten kan no skrivast slik

$\begin{array}{rcl} x^3-4x-x+4& < & 0\\ & & \\ \left(x+1\right)\left(x-1\right)\left(x-4\right)& <& 0\end{array}$

Vi tar no «stikkprøver» innanfor kvart intervall for å finne ut kva for eit forteikn uttrykket $\left(x+1\right)\left(x-1\right)\left(x-4\right)$ har i kvart av dei fire intervalla $⟨\leftarrow , -1⟩, ⟨-1, 1⟩, ⟨1, 4⟩ \mathrm{og} ⟨4, \to ⟩$.

For $x=-2$ får vi

$\left(-2+1\right)\left(-2-1\right)\left(-2-4\right)=\left(-1\right)·\left(-3\right)·\left(-5\right)$

Uttrykket er negativt.

For $x=0$ får vi

$\left(0+1\right)\left(0-1\right)\left(0-4\right)=\left(+1\right)·\left(-1\right)·\left(-4\right)$

Uttrykket er positivt.

For $x=2$ får vi

$\left(2+1\right)\left(2-1\right)\left(2-4\right)=\left(+3\right)·\left(+1\right)·\left(-2\right)$

Uttrykket er negativt.

For $x=5$ får vi

$\left(5+1\right)\left(5-1\right)\left(5-4\right)=\left(+6\right)·\left(+4\right)·\left(+1\right)$

Uttrykket er positivt.

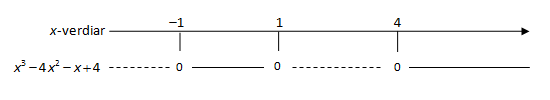
For å få ei oversikt over situasjonen set vi opp eit forteiknsskjema. Vår oppgåve var å finne ut for kva verdiar av x det var slik at $-4x^2<x-4-x^3$, det vil seie at $x^3-4x^2-x+4<0$. Løysinga på oppgåva blir då at x må være mindre enn −1 eller liggje mellom 1 og 4.

Løysinga er

$x\in ⟨\leftarrow , -1⟩\cup ⟨1, 4⟩$

I CAS i GeoGebra får vi

$\boxed{\begin{array}{c}\begin{array}{c}\begin{array}{ccc}& & \mathrm{Løys}\left(-4{\mathrm{x}}^2<\mathrm{x}-4-{\mathrm{x}}^3\right)\\ \overline{)1}& & \\ & & \to \left\{\mathrm{x}<-1, 1<\mathrm{x}<4\right\}\end{array}\end{array}\end{array}}$