Likningssett av første og andre grad
Då vi løyste likningssett med to likningar av første grad, brukte vi innsetjingsmetoden. Denne metoden kan vi også bruke her. Det luraste er då ofte å finne eit uttrykk for den eine ukjende ved hjelp av førstegradslikninga, og så setje dette uttrykket inn i andregradslikninga.
Vi har gitt likningssettet
Vi bruker førstegradslikninga til å finne eit uttrykk for
Vi set så uttrykket for inn i andregradslikninga
Legg merke til at vi her dividerer med -2 i siste linje for å få greiare tal å arbeide med når vi skal bruke abc-formelen.
Vi bruker abc-formelen til å løyse denne likninga
Vi set så desse løysingane inn i uttrykket for
Likningssettet har to sett med løysingar
( eller,
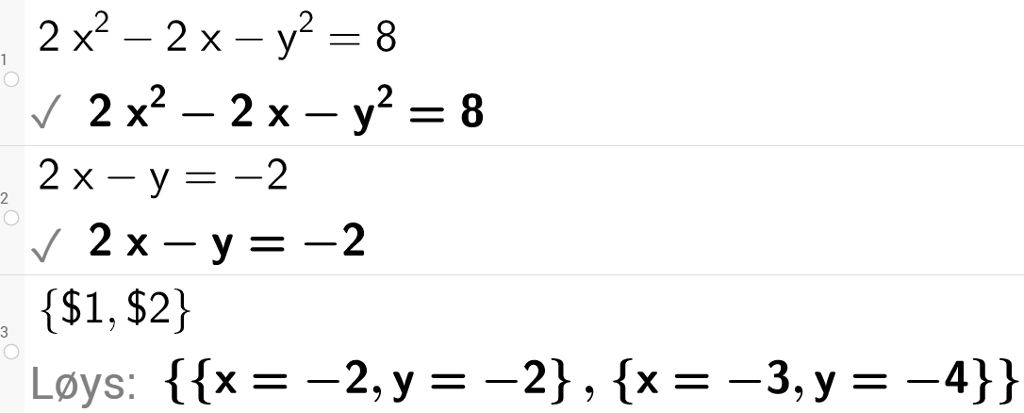
Nedanfor ser du korleis vi kan løyse likninga frå førre døme i GeoGebra.
Du markerer rute 1 og 2 for så å bruke knappen
I funksjonskapitlet skal du sjå korleis vi kan løyse likningssett grafisk.