Subject Material

Kvadratsetningene. Konjugatsetningen

Kvadratsetningene er svært sentrale i algebra.

De tre kvadratsetningene

Generelt har vi at

$\begin{matrix} (a + b) \cdot (c + d) = a c + a d + b c + b d \end{matrix}$

Hvordan blir resultatet dersom parentesuttrykkene er like eller nesten like?

Før du leser videre, kan du prøve selv å regne ut uttrykkene nedenfor og se om du kan finne en forenklet måte å regne ut slike uttrykk på.

$(a + b) (a + b) = \begin{matrix} \end{matrix} (a - b) (a - b) = \begin{matrix} \end{matrix} (a + b) (a - b) =$

Den første kvadratsetningen

Når vi multipliserer $(a + b)$ med seg selv, får vi kvadratet ${(a + b)}^{2}$ .

$\begin{array}{rcl} {(a + b)}^{2} & = & (a + b) \cdot (a + b) \\ = & a \cdot a + a \cdot b + b \cdot a + b \cdot b \\ = & a^{2} + a b + a b + b^{2} \\ = & a^{2} + 2 a b + b^{2} \end{array}$

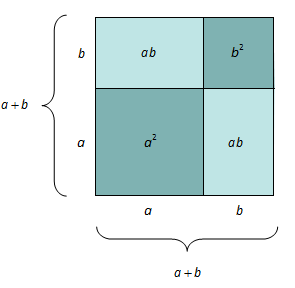
Et kvadrat med sidekanter a pluss b er delt i fire: ett kvadrat med sidekanter a, ett kvadrat med sidekanter b og to rektangler med sidekanter a og b. Illustrasjon. — Image: Olav Kristensen, Stein Aanensen / CC BY-SA

Når vi multipliserer ut parentesene, får vi to like ledd, $a b + a b$ , som vi slår sammen til $2 a b$ .

Geometrisk ser du at arealet av det store kvadratet ovenfor med sidelengder $a + b$ er lik summen av arealene av de to like store lyse rektanglene og de to mørke kvadratene.

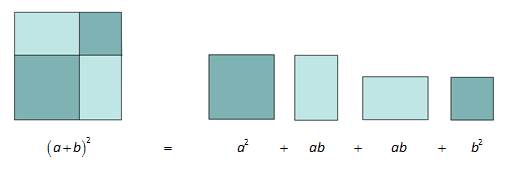
Et kvadrat med sidekanter a pluss b er delt i fire: ett kvadrat med sidekanter a, ett kvadrat med sidekanter b og to rektangler med sidekanter a og b. Ved siden av er disse mindre kvadratene og rektanglene stilt opp på rekke. Illustrasjon.

Dette resultatet er kjent som den første kvadratsetningen.

Den andre kvadratsetningen

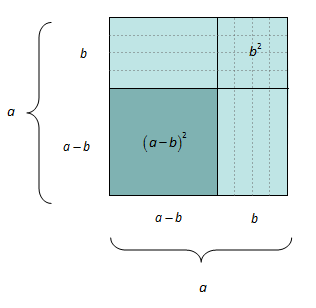
Et kvadrat med sidekanter a er delt i fire: ett kvadrat med sidekanter a minus b, ett kvadrat med sidekanter b og to rektangler med sidekanter a minus b og b. Illustrasjon. — Image: Stein Aanensen, Olav Kristensen / CC BY-NC-SA

Vi multipliserer videre $(a - b)$ med seg selv og får kvadratet ${(a - b)}^{2}$ .

$\begin{array}{rcl} {(a - b)}^{2} & = & (a - b) \cdot (a - b) \\ = & a \cdot a - a \cdot b - b \cdot a + b \cdot b \\ = & a^{2} - a b - a b + b^{2} \\ = & a^{2} - 2 a b + b^{2} \end{array}$

Her får vi to like ledd, $- a b - a b$ , som vi slår sammen til $- 2 a b$ .

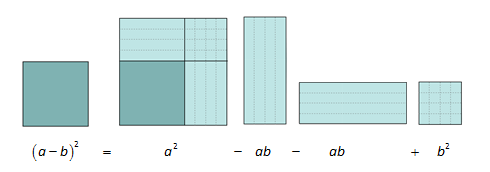
Et kvadrat med areal parentes a minus b parentes slutt i andre er det samme som ett kvadrat med areal a i andre minus to rektangler med areal a b pluss ett kvadrat med areal b i andre. Illustrasjon.

Ser du at vi kan illustrere dette geometrisk hvis vi tar utgangspunkt i et kvadrat med sider $a$ ?

Dette resultatet er kjent som den andre kvadratsetningen.

Konjugatsetningen

Vi multipliserer så $(a + b)$ med $(a - b)$ .

$\begin{array}{rcl} (a + b) \cdot (a - b) & = & a \cdot a - a \cdot b + b \cdot a - b \cdot b \\ (a + b) \cdot (a - b) & = & a^{2} - a b + a b - b^{2} \\ (a + b) \cdot (a - b) & = & a^{2} - b^{2} \end{array}$

Her får vi leddene $a b$ og $- a b$ , som til sammen blir lik null og faller bort.

Ser du at vi kan illustrere dette også geometrisk ved å starte med et kvadrat med sidekanter $a$ ?

$a^{2} - b^{2}$ tilsvarer det lyse området i den første figuren nedenfor.

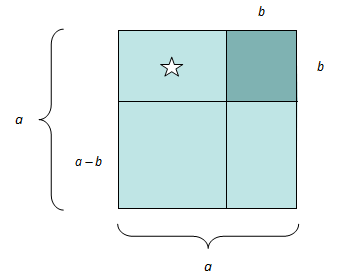
Hvis vi så tenker oss at vi flytter rektangelet som er merket med en stjerne, ser vi at det lyse området også tilsvarer $(a + b) (a - b)$ .

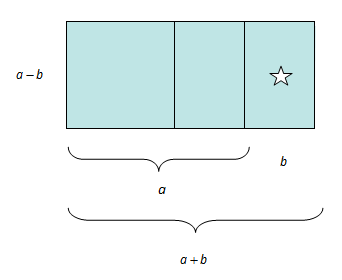
Et rektangel med sidekanter a minus b og a pluss b. Rektangelet er delt i tre ved at sidekanten som er a pluss b, er delt i tre: b, b og a minus b. Den ene delen med sidekanter b og a minus b er markert med ei stjerne. Illustrasjon.

Dette resultatet er kjent som konjugatsetningen, men kalles også den tredje kvadratsetningen (selv om den ikke beskriver et kvadrattall).

Oppsummering

Første kvadratsetning:

${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$

Andre kvadratsetning:

${(a - b)}^{2} = a^{2} - 2 a b + b^{2}$

Konjugatsetningen:

$(a + b) (a - b) = a^{2} - b^{2}$

Det er fristende å la være å pugge kvadratsetningene og heller multiplisere hvert ledd i den ene parentesen med hvert ledd i den andre parentesen. Det vil ikke være særlig lurt. Kvadratsetningene er nemlig spesielt nyttige til å faktorisere andregradsuttrykk, og da må du bruke dem motsatt vei.

Eksempel på bruk av kvadratsetningene

$\begin{array}{rcl} \begin{array}{rcl} 4 {(x + 2)}^{2} & + & {(2 x - 3)}^{2} - 3 (x - 2) (x + 2) \end{array} \\ = & 4 (x^{2} + 2 \cdot x \cdot 2 + 2^{2}) + ({(2 x)}^{2} - 2 \cdot 2 x \cdot 3 + 3^{2}) - 3 (x^{2} - 2^{2}) \\ = & 4 (x^{2} + 4 x + 4) + (4 x^{2} - 12 x + 9) - 3 (x^{2} - 4) \\ = & (4 x^{2} + 16 x + 16) + (4 x^{2} - 12 x + 9) - (3 x^{2} - 12) \\ = & 4 x^{2} + 16 x + 16 + 4 x^{2} - 12 x + 9 - 3 x^{2} + 12 \\ = & 5 x^{2} + 4 x + 37 \end{array}$

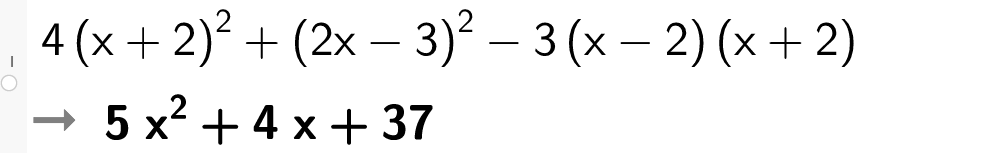
Utklipp fra CAS i GeoGebra. På linje 1 er det skrevet 4 parentes x pluss 2 parentes slutt i andre pluss parentes 2 x minus 3 parentes slutt i andre minus 3 parentes x minus 2 parentes slutt parentes x pluss 2 parentes slutt. Resultatet er 5 x i andre pluss 4 x pluss 37. Skjermutklipp.

Med CAS i GeoGebra:

CC BY-SAWritten by: Olav Kristensen and Stein Aanensen.

Last revised date 08/22/2024