Beregning av sirkulasjonstrykk
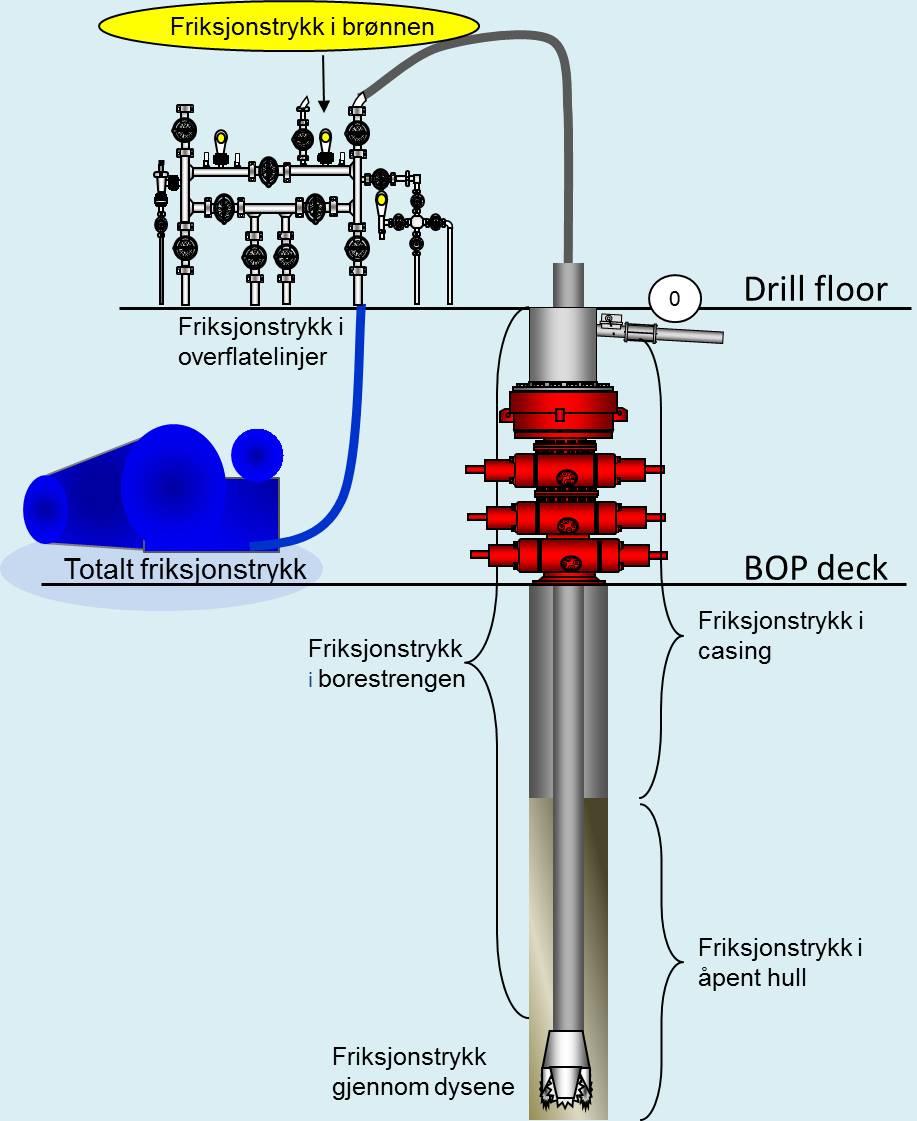
Friksjonstrykk omtales som trykktap, ettersom trykket blir mindre og mindre desto lenger ut i systemet man måler. I enden er det 0 bar dersom væsken går ut i et åpent anlegg.
Eksempel
En brønn er 3460 m MD (lang) og 3200 meter TVD (vertikal). Brønnen er fylt med boreslam med 1,31 sg. Ved normal sirkulasjon er det et trykktap på 0,04 bar/m i borestrengen og 0,008 bar/m i annulus. Gjennom dysene er det et trykktap på 30 bar.
Hva blir det totale trykktapet gjennom systemet?
Svar:
I borestrengen: 0,04 bar/m ∙ 3460 m = 138,4 bar
I dysene: 30 bar
I annulus: 0,008 bar/m ∙ 3460 m = 27,7 bar
Totalt trykktap: 138,4 + 30 + 27,7 = 196,1 bar.
Det totale trykktapet er pumpetrykket som må til for å sirkulere væsken gjennom systemet.
Hva er trykket i bunnen av brønnen (i annulus) når vi sirkulerer boreslammet?
Svar:
I bunnen av brønnen er det friksjonen i annulus som gjenstår.
Trykket vil være det hydrostatiske trykket sammen med friksjonstrykket i annulus.
=
Friksjonstrykket endres når følgende betingelser endres:
- væskens hastighet og strømningsmønster
- viskositet
- densitet
- innvendig overflate og retningsendringer i rør
- lengden på sirkulasjonssløyfen
Her skal vi beregne noen av disse endringene.
Regneoppgave 1
En brønn er 2500 meter lang (mMD) og dyp (mTVD). Det betyr at den er vertikal.
Siste casing er satt på 2300 meter. I brønnen er det borevæske med densitet 1,20 sg. Friksjonstrykkgradienten er 0,02 bar/meter i borerørene og 0,001 bar/meter i ringrommet når vi sirkulerer med 40 spm. Trykkfallet gjennom dysene i borekronen er 20 bar.
1) Hva er det hydrostatiske trykket på bunnen av brønnen?
Vi starter sirkulasjonen forsiktig og lar pumpen svive med 40 spm.
2) Hva er trykket på overflaten ved pumpen?
Vi beregner summen av all friksjon i sirkulasjonssystemet.
3) Hva er trykket i bunnen av brønnen (i ringrommet)?
Vis utregningene.
Tester og beregninger har bekreftet at når væskestrømmen (Q) fordobles, øker friksjonstrykket (p) med ca. fire ganger. Det kan uttrykkes i formelen
I formelen viser 1 den gamle verdien og 2 den nye verdien.
I realiteten gjelder formelen når det er snakk om rent vann i ideelle forhold. Med boreslam viser det seg at eksponenten er nærmere 1,86, men vi kan regne med 2 ettersom det utgjør minimale forskjeller. Væskestrøm kan oppgis i liter per minutt, eller som slag per minutt (SPM).
Regneoppgave 2
Vi fortsetter med den samme brønnen som i oppgave 1.
Nå økes pumperaten til 80 SPM.
4) Hva er trykket på overflaten ved pumpen (totalt friksjonstrykk)?
Nå kan vi beregne det nye trykket ved hjelp av det vi hadde med forrige pumperate:
5) Hva er trykket i bunnen av brønnen (i ringrommet)?
Her beregner vi nytt friksjonstrykk i ringrommet først og legger sammen med det hydrostatiske trykket:
Vis utregningene.
Fordypning:
i) Hva er den nye friksjonsfaktoren i bar per meter i ringrommet?
ii) Hva er den nye friksjonsfaktoren i borestrengen?
iii) Hva er den nye friksjonen i dysene i borekronen?
Når densiteten endres, påvirker det trykket direkte.
Det ser vi av formelen
Regneoppgave 3
Vi fortsetter fra oppgave 2. Vi veier opp boreslam til 1,25sg og sirkulerer slik at hele brønnen fylles med det nye slammet. Pumperaten er fremdeles 80 SPM.
6) Hva er trykket på overflaten ved pumpen (totalt friksjonstrykk)?
Nå regner vi om friksjonstrykket på grunn av endringen i densitet. Vi bruker forrige samlet friksjonstrykk som pf1 for å finne det nye friskjonstrykket pf2:
7) Hva er trykket i bunnen av brønnen (i ringrommet)?
Nå er både friksjonstrykket i ringrommet og det hydrostatiske trykket endret:
Vis utregningene.
Fordypning:
iv) Hva er trykket ved casingskoen?
Etter hvert som brønnens lengde øker, vil friksjonstrykket også øke.
Regneoppgave 4
Vi har boret videre med det nye slammet (1,25 sg), og brønnen er nå 3200 m MD/TVD.
Vi sirkulerer med 40 SPM.
8) Hva er trykket på overflaten ved pumpen (totalt friksjonstrykk)?
Vi tar hensyn til ny lengde med nytt slam og beregner summen av friksjonen i hele systemet.
9) Hva er trykket i bunnen av brønnen (i ringrommet)?
Vis utregningene.
Fordypning:
v) Vi øker pumperaten til 80 SPM. Regn ut friksjonstrykket i bunnen av brønnen til ECD.