Kostnads-, inntekts- og overskotsfunksjon

Inntektene og kostnadene til ei bedrift vil variere med kor mykje som blir produsert. Det vil som regel vere slik at jo meir som blir produsert, jo høgare blir både inntekter og kostnader. Overskotet til ei bedrift aukar ikkje nødvendigvis sjølv om bedrifta får auka salet. Det hjelper ikkje at bedrifta tener 5 000 kroner meir ved eit auka sal av nokre varer dersom det kostar 10 000 kroner å produsere dei ekstra varene. Bedrifta må derfor ha god oversikt over korleis kostnadene varierer med kor mykje dei produserer.

Overskotet ei bedrift får, kan vi rekne ut ved å trekke kostnaden ved produksjonen frå inntekta ved salet. Dersom det kostar bedrifta 20 000 kroner å produsere ei viss varemengde og inntekta frå salet er 30 000 kroner, vil overskotet bli

$$ 30 000 \mathrm{kr}-20 000 \mathrm{kr}=10 000 \mathrm{kr}$$

Vi kan derfor lage oss følgande formel:

Overskot $$ \mathrm{=}$$ Inntekt $$ -$$ Kostnad

Husk at inntekt ikkje er pengar dei kan stikke rett i lomma! Inntektene må brukast til å betale kostnadene. Så er håpet at det er igjen noko etter at kostnadene er betalte slik at dei går med overskot.

Prøv sjølv

Kva er inntekta av eit sal dersom overskotet er 45 000 kroner og kostnadene ved produksjonen er 25 000 kroner?

Dersom vi kan lage funksjonar for inntektene og kostnadene, får vi ei god oversikt over korleis overskotet kan variere med tal. Dersom $$ x$$ står for produsert mengde varer, kan vi setje opp følgande:

• Kostnadsfunksjon: $$ K\left(x\right)$$

• Inntektsfunksjon: $$ I\left(x\right)$$

• Overskotsfunksjon: $$ O\left(x\right)$$

Set opp eit generelt uttrykk for overskotsfunksjonen $$ O\left(x\right)$$ ved hjelp av $$ K\left(x\right)$$ og $$ I\left(x\right)$$.

Klasse 3STB ønske å starte ei elevbedrift for å produsere eit treningsapparat dei kallar Multiform. Vi skal bruke dette som døme.

Kostnadsfunksjon

Klassen lar $x$ vere talet på produserte einingar per veke. Dei leiger eit produksjonslokale til 11 000 kroner per veke. Prisen inkluderer utgifter til lys og varme. Denne kostnaden er ikkje avhengig av kor mange einingar som blir produserte, og kan derfor vere eit konstantledd i ein kostnadsfunksjon.

For kvart treningsapparat som blir produsert, går det med ei bestemd mengde komponentar, som blir kjøpt inn til einingsprisar. Det blir òg kravd eit visst tal arbeidstimar for montering av kvar eining. Klassen reknar desse utgiftene til å vere 150 kroner per eining, og i ein kostnadsfunksjon gir dette førstegradsleddet 150$x$.

Klassen reknar med at det enkelte veker blir nødvendig med ekstra høg produksjon. Då kan det bli nødvendig med overtid, og kanskje dei må setje fleire elevar i arbeid med produksjonen. Slike ekstrautgifter vil vere låge ved liten produksjon og store ved høg produksjon. Læraren til elevane foreslår derfor at kostnadsfunksjonen òg skal innehalde leddet $3x^2$, for då vil kostnadene auke raskare når $$ x$$ blir stor.

Alle er samde om at dei med normal innsats vil klare å produsere og selje 130 treningsapparat per veke, men også at dei med nokre grep kan klare å produsere og selje 150. Det betyr at definisjonsområdet til kostnadsfunksjonen vil vere frå og med 0 til og med 150.

Dersom klassen tek utgangspunkt i dette, vil kostnadene per veke ved produksjon av $x$ treningsapparat kunne beskrivast med polynomfunksjonen $K$ gitt ved

$$ K\left(x\right)=3x^2+150x+11 000\begin{array}{ccc}& & \end{array} D_K=\left[0,150\right]$$

Elevane er samde om at produksjonskostnadene foreløpig er særs usikre. Dei er derfor innstilte på å justere modellen når dei ser dei verkelege utgiftene.

Einingskostnad

Dersom vi ønsker å rekne ut kostnaden per eining, må vi dele dei totale kostnadene på talet på produserte einingar. Dette gir følgande funksjon for einingskostnaden i dømet over:

$$ E\left(x\right)=\frac{K\left(x\right)}{x}=\frac{3x^2+150x+11 000}{x}$$

Inntektsfunksjon

Klassen vurderer kva pris dei skal setje på Multiform. Elevane er einige om at 800 kroner er ein passe pris på produktet.

Kva blir inntektsfunksjonen $$ I\left(x\right)$$ ved sal av $$ x$$ einingar ut frå dette?

Trym er litt skeptisk og seier: "Ein slik funksjon passar dårleg overeins med at når det blir god tilgang på ei vare, vil prisen gå ned. Ein annan ting er at for å oppnå eit stort sal er vi avhengige av å selje større parti til sportsbutikkar, som sel vidare for oss. Då må vi nok rekne med ein lågare pris enn om vi sel alt sjølv."

Klassen er heilt einig med Trym, og læraren til elevane foreslår at dei må ha eit ledd av typen $$ x^2$$ i inntektsfunksjonen slik som i kostnadsfunksjonen. Dette leddet må trekkast frå for at inntektene skal bli mindre når $$ x$$ blir stor. Dei prøver derfor med inntektsfunksjonen $I$ gitt ved

$I\left(x\right)=800x-2x^2$

Elevane teiknar grafen til $I$ i same koordinatsystem som grafen til $K$ og finn skjeringspunkta mellom dei to grafane.

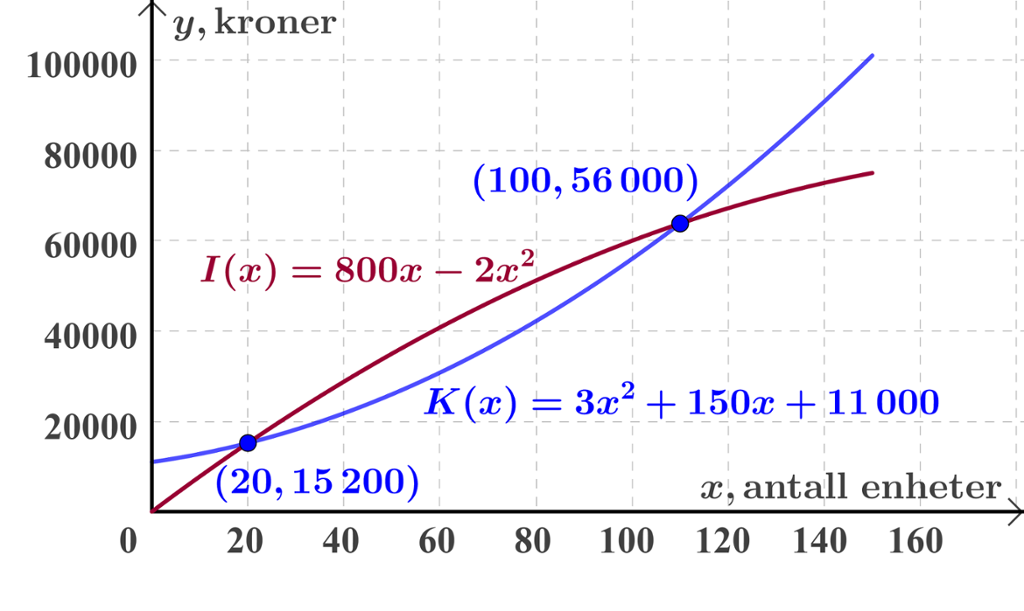
Hjelp elevane i 3STB med å tolke den grafiske framstillinga. Skriv ned nokre punkt om kva du kan lese ut av diagrammet.

Overskotsfunksjon

For å finne kor mange treningsapparat elevbedrifta skal produsere for å oppnå størst overskot, kan dei finne overskotsfunksjonen.

Hjelp elevane å finne overskotsfunksjonen.

Klassen teiknar grafen til overskotsfunksjonen $O$ i det same koordinatsystemet som grafane til $K$ og $I$. Då skriv dei berre O(x) = I - K i algebrafeltet til GeoGebra sidan dei har lagt inn inntekts- og kostnadsfunksjonen frå før.

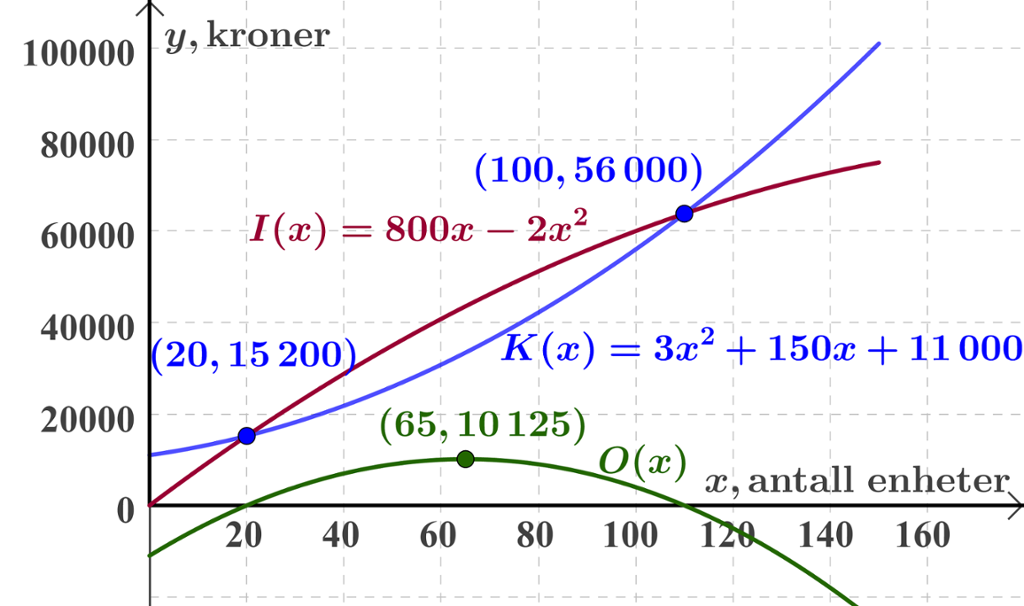
Det største overskotet må vere der grafen til $$ O$$ har eit toppunkt. Med verktøyet eller kommandoen "Ekstremalpunkt" finn elevane toppunktet til overskotsfunksjonen. Resultatet viser at overskotet er størst ved ein produksjon på 65 einingar. Då er overskotet per veke på 10 125 kroner.

Vi kan òg finne det største overskotet med CAS.

Treng vi å ha med utrekninga i linje 5?