Gruppert datamateriale. Histogram

I Noreg blir det kvart år gjennomført ei statistisk undersøking av høgda til vernepliktige rekruttar. Her ville frekvenstabellen ha vorte veldig stor dersom ein tek med alle moglege høgder, og derfor er høgdene inndelte i grupper eller klassar.

Tala i tabellen nedanfor er henta frå Statistisk sentralbyrå: 4.22 Vernepliktige, etter høyde. Prosent (ssb.no).

Vi ser nærare på tala for 1910. I tabellen nedanfor har vi late som om det var akkurat 1 000 rekruttar i 1910. Sidan det var 32,3 prosent mellom 170 og 155 cm, betyr det at det var 323 vernepliktige i denne klassen, og tilsvarande for dei andre klassane. Vi har valt å plassere alle med høgde under 165 cm i ein klasse med høgder frå 155 cm til 165 cm.

Klassane er markerte som halvopne intervall. Til dømes er klassen frå og med 175 cm til 180 cm markert med det halvopne intervallet $[175, 180\rangle$. Ein rekrutt med høgda 175 cm høyrer til denne klassen, men ikkje ein rekrutt med høgde 180 cm. For denne klassen er 175 cm nedre klassegrense, og 180 cm er øvre klassegrense.

I kva klasse skal ein rekrutt med høgde 185 cm plasserast?

Vi ønskjer å presentere datamaterialet frå tabellen i eit diagram. Då får vi eit problem. Den første klassen, som går frå 155 cm til 165 cm, er nemleg dobbelt så brei som den neste. Eit vanleg søylediagram vil gi ei søyle som er dobbelt så høg i forhold til om vi hadde fordelt dei 128 rekruttane i to klassar med lik klassebreidde.

I staden for å dele den store klassen i to klassar, løyser vi problemet ved å rekne ut "kor mange rekruttar det er på kvar centimeter" i dei ulike klassane. I klassen $[155, 165\rangle$ er det 128 rekruttar. Klassebreidda er 10 cm. Det vil seie at det i gjennomsnitt er  $\frac{128}{10}=12,8$  rekruttar per centimeter i denne klassen. I klassen $[165, 170\rangle$ er det 260 rekruttar. Klassebreidda er 5 cm. Det vil seie at det er  $\frac{260}{5}=52$  rekruttar per centimeter i denne klassen.

Kor mange rekruttar er det per centimeter for klassen [180, 185⟩?

Talet på rekruttar per centimeter kallar vi for histogramhøgde (frekvens dividert på klassebreidde), og vi bruker dette som høgde på søyler i eit spesielt diagram som vi kallar histogram.

Histogrammet teiknar vi i GeoGebra med kommandoen "Histogram(<Liste med klassegrenser>,<Liste med høgder>)" i algebrafeltet. Lista med klassegrenser må innehalde tala 155, 165, 170 og så vidare til og med 200. Vi bruker reknearkdelen i GeoGebra til å rekne ut histogramhøgdene. Dersom vi lagar listene med tala og kallar dei "klassegrenser" og "høgder", lagar vi histogrammet med kommandoen

Histogram(klassegrenser,høgder)

Merk at det blir eitt tal meir i lista over klassegrenser enn i lista over histogramhøgder.

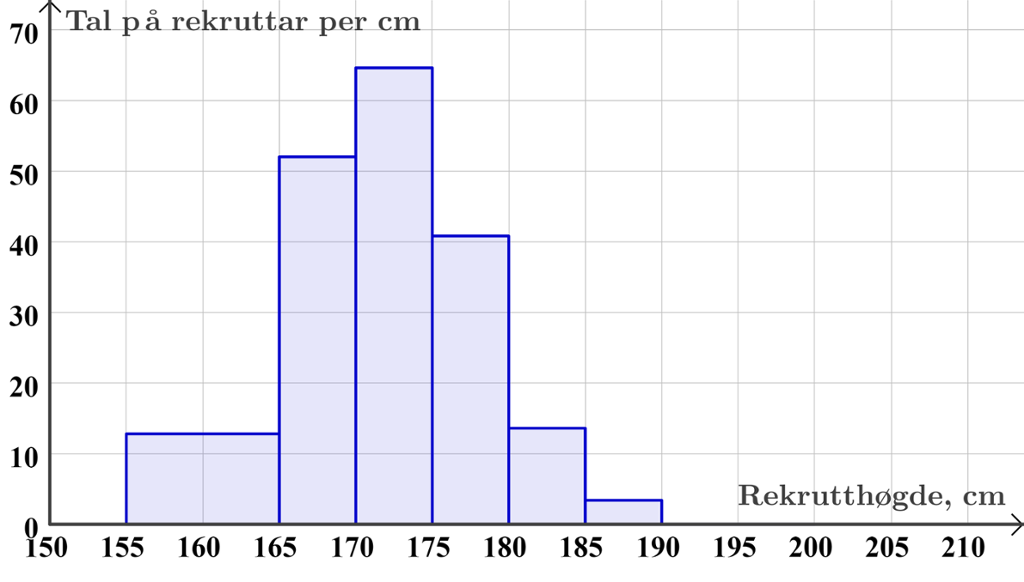
I eit histogram må vi multiplisere histogramhøgda med klassebreidda for å finne talet på rekruttar i klassen.

I klassen $[155, 165⟩$ er histogramhøgda 12,8. Talet på rekruttar i klassen er

$12,8·10=128$

I klassen $[165, 170⟩$ er histogramhøgda 52. Talet på rekruttar i klassen er

$52·5=260$

Lag histogrammet over med GeoGebra. Bruk reknearkdelen i GeoGebra til å rekne ut histogramhøgdene.

Løysing

Reknearkdelen i GeoGebra kan sjå slik ut:

Formelvisinga av reknearket ser slik ut:

No kan vi lage lister av klassegrensene i kolonne B og histogramhøgdene i kolonne E og bruke kommandoen "Histogram()" som vist lenger opp.

For å få til histogrammet på biletet over der $$ y$$-aksen kryssar $$ x$$-aksen for  $$ x=150$$  i staden for i origo, har vi gått til innstillingar for grafikkfeltet, valt fana "yAkse" og late $$ y$$-aksen krysse ved 150. Det er òg under fanene "xAkse" og "yAkse" vi kan skrive på aksetitlar ("Namn på aksen:").

Nedanfor kan du laste ned eit GeoGebra-ark med tala i reknearkdelen og det ferdige histogrammet.

Filer

• Histogram over rekrutthøgde(GGB)

Statistisk sentralbyrå (u.å.). 4.22 Vernepliktige, etter høyde. Prosent [Tabell]. Hentet 30. september 2021 https://www.ssb.no/a/histstat/tabeller/4-22.html