Hopp til innhald

Fagstoff

Multiplikasjon av sannsyn

For å finne sannsynet til samansette hendingar kan vi multiplisere sannsynet for enkelthendingane. Vi må ta omsyn til om hendingane er avhengige eller uavhengige.

Produktsetninga for uavhengige hendingar

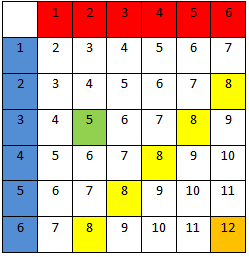
Tabell som viser summen av eitt kast med to terningar for alle moglege utfall. Illustrasjon.

Vi har tidlegare sett på forsøket "kast med to terningar".

Ved å bruke regelen om gunstige over moglege kan vi finne sannsynet for å få summen 12, det vil seie seksar på begge terningane.

$P (Seksar på begge terningane) = \frac{g}{m} = \frac{1}{36}$

Sannsynet for å få ein seksar når vi kastar den raude terningen, er $\frac{1}{6}$ . Sannsynet for å få ein seksar når vi kastar den blå terningen, er òg $\frac{1}{6}$ . Dette gjeld uavhengig av om det vart ein seksar på raud terning eller ikkje. Om vi kastar raud terning først og får ein seksar, endrar ikkje dette sjansane for å få ein seksar på den blå terningen.

Vi seier at hendingane "å få seksar på raud terning" og "å få seksar på blå terning" er uavhengige hendingar.

Vi såg ovanfor at sannsynet for å få seksar i begge kasta er lik $\frac{1}{36}$ . Dette sannsynet får vi òg ved å multiplisere sannsyna for å få seksar på kvar av terningane.

$\begin{array}{rcl} P (Seksar på raud terning og seksar på blå terning) \\ = & P (Seksar på raud terning) \cdot (Seksar på blå terning) \\ = & \frac{1}{6} \cdot \frac{1}{6} = \frac{1}{36} \end{array}$

Dette gjeld generelt og blir kalla produktsetninga for uavhengige hendingar.

To hendingar er uavhengige dersom ei opplysning om at den eine har hendt ikkje endrar sannsynet for at den andre skal hende.

For to uavhengige hendingar $A$ og $B$ er

$P (A og B) = P (A) \cdot P (B)$

$A$ og $B$ betyr her at både $A$ og $B$ hender.

Vi erstattar orda "og" med symbolet " $\cap$ ", og $A \cap B$ les vi som

" $A$ snitt $B$ ". Vi får

$P (A \cap B) = P (A) \cdot P (B)$

Setninga gjeld òg for ein serie av hendingar.

Tippekupong

Utsnitt frå tippekupong som viser ein tabell over 12 ulike fotballkampar, for det meste med engelske lag. Til høgre kan ein krysse av for H, U eller B på alle kampane. Foto.

Kor stor er sannsynet for å få 12 rette i fotballtipping når vi fyller ut éi rekkje på ein tippekupong heilt tilfeldig?

Løysing

Vi kan oppfatte dette som 12 hendingar. Kvar kamp kan ende med heimesiger (H), uavgjort (U) eller bortesiger (B). I kvar kamp er sannsynet for å tippe rett lik $\frac{1}{3}$ .

Sannsynet for å tippe rett i kvar kamp er den same uavhengig av om vi har tippa rett eller feil i tidlegare kampar.

Vi har altså 12 uavhengige hendingar.

Sannsynet for å tippe 12 rette er då lik $\frac{1}{3}$ multiplisert med seg sjølv 12 gonger.

$\begin{array}{rcl} P (12 rette) & = & \frac{1}{3} \cdot \frac{1}{3} \cdot \frac{1}{3} \cdot \frac{1}{3} \cdot \frac{1}{3} \cdot \frac{1}{3} \cdot \frac{1}{3} \cdot \frac{1}{3} \cdot \frac{1}{3} \cdot \frac{1}{3} \cdot \frac{1}{3} \cdot \frac{1}{3} \\ = & {(\frac{1}{3})}^{12} = \frac{1}{531441} \approx 0, 0000019 = 0, 00019 % \end{array}$

Under kan du sjå ein film som viser produktsetninga for uavhengige hendingar.

Video: Olav Kristensen

Sannsyn med vilkår – den generelle produktsetninga

Caps med lappar med tal snudd opp ned. Foto.

Celine og Maren trekkjer kvar sin lapp frå ein hatt som inneheld fem lappar med tala frå 1 til 5.

Vi definerer hendinga.

$A$ : På Celine sin lapp står det eit partal.
$B$ : På Maren sin lapp står det eit partal.

Dersom Celine trekkjer den første lappen, er det i hatten 2 lappar med partal og 3 lappar med oddetal. Sannsynet for å trekkje ein lapp med partal er

$P (A) = \frac{2}{5}$

Dersom Celine trekkjer eit partal, er det igjen 1 lapp med partal og 3 lappar med oddetal når Maren trekkjer, og sannsynet for at Maren òg trekkjer eit partal, er lik $\frac{1}{4}$ .

Dersom Celine ikkje trekkjer eit partal, er det igjen 2 lappar med partal og 2 lappar med oddetal når Maren trekkjer, og sannsynet for at Maren trekkjer eit partal, er lik $\frac{2}{4} = \frac{1}{2}$ .

Sannsynet for $B$ avheng av om hendinga $A$ hender eller ikkje. Vi seier at hendingane $A$ og $B$ er avhengige.

Sannsynet for at $B$ hender når vi veit at $A$ har hendt, er lik $\frac{1}{4}$ .

Sannsynet for at $B$ hender når vi veit at $A$ ikkje har hendt, er lik $\frac{2}{4} = \frac{1}{2}$ .

Vi kallar dette sannsyn med vilkår. Vi bruker skrivemåten $P (B | A)$ , som vi les som "sannsynet for $B$ gitt $A$ ". Vi har at

$P (B | A) = \frac{1}{4}$

Vi bruker skrivemåten for ikkje $A$ . Då er

$P (B | \bar{A}) = \frac{1}{2}$

Sannsynet for at det skal stå eit partal på begge lappane, det vil seie at både hending $A$ og hending $B$ hender, finn vi ved å multiplisere sannsyna:

$P (A \cap B) = P (A) \cdot P (B | A) = \frac{2}{5} \cdot \frac{1}{4} = \frac{1}{10}$

Dersom Maren trekkjer den første lappen, gjeld tilsvarande at

$P (B) = \frac{2}{5}$

Tilsvarande blir no

$P (A | B) = \frac{1}{4} og P (A | \bar{B}) = \frac{1}{2}$

Sannsynet for at det skal stå eit partal på begge lappane, det vil seie at både hending $B$ og hending $A$ hender, finn vi ved å multiplisere sannsyna:

$P (B \cap A) = P (B) \cdot P (A | B) = \frac{2}{5} \cdot \frac{1}{4} = \frac{1}{10}$

Sannsyn med vilkår

Sannsynet for at $B$ hender når vi veit at $A$ har hendt, skriv vi som $P (B | A)$ , og det blir lese som "sannsynet for $B$ gitt $A$ ". Vi kallar det for sannsyn med vilkår.

Den generelle produktsetninga for sannsyn

Sannsynet for at to hendingar, både $A$ og $B$ skal hende, er

$P (A \cap B) = P (A) \cdot P (B | A)$

For uavhengige hendingar er $P (B | A) = P (B), og P (A \cap B) = P (A) \cdot P (B)$ .

Under kan du sjå ein film om sannsyn med vilkår.

Video: Olav Kristensen

CC BY-SASkrive av Olav Kristensen og Stein Aanensen.

Sist fagleg oppdatert 14.12.2020

Læringsressursar

Grunnleggande sannsynsrekning