Drøfting av polynomfunksjonar

Å finne ut kvar grafen til ein funksjon stig og kvar grafen søkk, blir kalla for å drøfte monotonieigenskapane til funksjonen.

Å drøfte ein funksjon betyr gjerne at vi skal undersøke monotonieigenskapane og bestemme topp- og botnpunkt på grafen. Ei fellesnemning for topp- og botnpunkt er ekstremalpunkt.

Her kjem ei utfordring:

Teikn grafen til tredjegradsfunksjonen $f$ gitt ved

$f\left(x\right)=\frac{1}{3}{x}^3-\frac{1}{2}{x}^2-2x+1$

Teikn deretter tangentar til grafen for nokon $x$-verdiar mellom $-2$ og $3$.

Undersøk om det er ein samanheng mellom stigningstalet til tangentane og om grafen stig, søkk eller har topp- eller botnpunkt.

Her kan du sjå at

• stigningstalet til tangenten er positivt når grafen stig for stigande $x$-verdiar
• stigningstalet til tangenten er negativt når grafen søkk for stigande $x$-verdiar
• stigningstalet til tangenten er null i topp- og botnpunkt for stigande $x$-verdiar
  
  

Sidan stigningstalet til tangenten er lik den deriverte til funksjonen, betyr dette følgande:

Dette betyr at vi kan finne ut for kva verdiar av $x$ grafen til ein funksjon stig, for kva verdiar av $x$ han søkk og når han har topp- eller botnpunkt ved å sjå på forteiknet til den deriverte. Vi viser dette gjennom nokre eksempel.

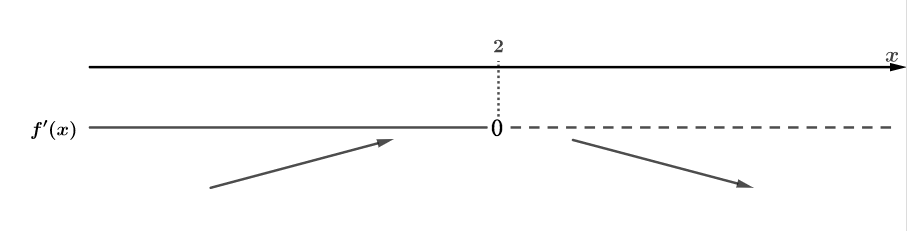
Vi skal finne eventuelle ekstremalpunkt (topp- og botnpunkt) til ein funksjon der den deriverte funksjonen har følgande graf:

Løysing

Den deriverte funksjonen, $f^{\text{'}}$, har nullpunkta $x=-2$ og $x=\frac{1}{3}$.

For $x<-2$ er $f^{\text{'}}$ positiv, som betyr at grafen til $f$ stig. For $-2<x<\frac{1}{3}$ er $f^{\text{'}}$ negativ, som betyr at grafen til $f$ søkk. Det betyr at funksjonen $f$ har eit toppunkt for $$ x=-2$$.

For $-2<x<\frac{1}{3}$ er $f^{\text{'}}$ negativ, som betyr at grafen til $f$ søkk. For $x>\frac{1}{3}$ er $f^{\text{'}}$ positiv, som betyr at grafen til $f$ stig. Det betyr at funksjonen $f$ har eit botnpunkt for $$ x=\frac{1}{3}$$.

Vi teiknar grafen til ein funksjon som passar med opplysningane ovanfor:

Drøft monotonieigenskapane til ein funksjon der den deriverte funksjonen har grafen under til høgre.

Funksjonen $f$ har nullpunkt $x=\frac{1}{2}$ og $f\left(2\right)=1$.

Lag ei skisse av grafen til $f$.

Løysing

Vi kan setje opp forteiknslinja til $f^{\text{'}}\left(x\right)$:

Vi legg merke til at den deriverte ikkje skifter forteikn i nullpunktet. Den deriverte er positiv for $x\ne 2$. Det betyr at funksjonen er veksande både før og etter at $x=2$. Grafen til funksjonen $f$ har verken topp- eller botnpunkt for $x=2$, men sidan den deriverte er lik null, er tangenten til grafen horisontal for $x=2$. Eit slikt punkt på grafen blir kalla for eit terrassepunkt.

Nedanfor har vi teikna ei skisse av grafen til $f$.

Eit stasjonært punkt er eit toppunkt eller eit botnpunkt dersom $f^{\text{'}}\left(x\right)$ skifter forteikn i punktet.

Eit terrassepunkt er eit stasjonært punkt der funksjonen ikkje endrar seg frå veksande til minkande eller frå minkande til veksande. Det vil seie at den deriverte ikkje skiftar forteikn.

På grunnlag av den deriverte funksjonen $f^{\text{'}}\left(x\right)=-2x+4$ skal vi finne når grafen til funksjonen $f$ stig og når han søkk. Vi skal òg finne eventuelle topp- eller botnpunkt. Vidare skal vi utan hjelpemiddel finne eit mogleg funksjonsuttrykk for $f$.

Løysing

Vi set $f^{\text{'}}\left(x\right)=0$.

$\begin{array}{rcl}-2x+4& = & 0\\ -2x& =& -4\\ x& =& 2\end{array}$

Det er berre i nullpunkta at uttrykket for den deriverte kan skifte forteikn. Vi vel derfor tilfeldige $x$-verdiar i kvart av dei aktuelle intervalla $⟨\leftarrow , 2⟩$ og $⟨2, \to ⟩$ for å sjå om uttrykket er positivt eller negativt.

$\begin{array}{l}{f}^{\text{'}}\left(0\right)=-2·0+4=4>0\\ \\ f^{\text{'}}\left(3\right)=-2·3+4=-2<0\end{array}$

Vi kan då setje opp forteiknslinja til $f^{\text{'}}\left(x\right)$:

Vi ser av forteiknslinja at grafen veks for $x\in \langle \leftarrow , 2\rangle$ , og at grafen søkk når $x\in ⟨2, \to ⟩$.

Grafen til $f\left(x\right)$ har derfor eit toppunkt når $x=2$.

Vi veit at viss toppunktet ligg over $x$-aksen, så har grafen to nullpunkt. Grafen er òg symmetrisk om symmetrilinja som går gjennom toppunktet. Ein funksjon med nullpunkt $x=1$ og $x=3$ og med negativ koeffisient før andregradsleddet, vil derfor oppfylle krava.

Ein mogleg funksjon er derfor

$\begin{array}{rcl}f\left(x\right) & =& -\left(x-1\right)\left(x-3\right)\\ & =& -\left(x^2-3x-x+3\right)\\ & =& -x^2+4x-3\end{array}$

Toppunktet for denne funksjonen er

$(2, f(2\left)\right)=\left(2, -2^2+4·2-3\right)=\left(2, -4+8-3\right)=(2, 1)$

Vi teiknar grafen i GeoGebra og ser at det vi har funne utan hjelpemiddel er riktig.

Vi skal drøfte monotonieigenskapane til $f$ utan hjelpemiddel og finne eventuelle topp- og botnpunkt på grafen til $f$ gitt ved

$f\left(x\right)=-\frac{1}{4}{x}^3-\frac{5}{8}{x}^2+\frac{1}{2}x+\frac{3}{8}$

I tillegg skal vi finne nok opplysningar om funksjonen til å teikne ei skisse av grafen.

Løysing

Vi deriverer funksjonen.

$$ \begin{array}{rcl}{f}^{\text{'}}\left(x\right) & =& -\frac{1}{4}·3·x^{3-1}-\frac{5}{8}·2·x^{2-1}+\frac{1}{2}·1·x^{1-1}+0\\ & =& -\frac{3}{4}{x}^2-\frac{5}{4}x+\frac{1}{2}\end{array}$$

Vi set $f^{\text{'}}\left(x\right)=0$.

$\begin{array}{rcl}-\frac{3}{4}{x}^2-\frac{5}{4}x+\frac{1}{2}& = & 0\\ x& =& \frac{-\left(-{\displaystyle \frac{5}{4}}\right)\pm \sqrt{{\left(-{\displaystyle \frac{5}{4}}\right)}^2-4·\left(-{\displaystyle \frac{3}{4}}\right)·{\displaystyle \frac{1}{2}}}}{2·\left(-{\displaystyle \frac{3}{4}}\right)}\\ x& =& \frac{{\displaystyle \frac{5}{4}}\pm \sqrt{{\displaystyle \frac{25}{16}}+{\displaystyle \frac{24}{16}}}}{-{\displaystyle \frac{3}{2}}}\\ x& =& \frac{{\displaystyle \frac{5}{4}\pm \frac{7}{4}}}{-{\displaystyle \frac{3}{2}}}=-\frac{5\pm 7}{6}\\ x& =& \frac{1}{3} \mathrm{eller} x=-2\\ & & \end{array}$

Det er berre i nullpunkta at uttrykket for den deriverte kan skifte forteikn. Vi vel derfor tilfeldige verdiar i kvart av dei aktuelle intervalla $⟨\leftarrow , -2⟩, ⟨-2, \frac{1}{3}⟩$ og $⟨\frac{1}{3}, \to ⟩$ for å sjå om uttrykket er positivt eller negativt.

$\begin{array}{rcl}{f}^{\text{'}}\left(-3\right) & =& -\frac{3}{4}{\left(-3\right)}^2-\frac{5}{4}\left(-3\right)+\frac{1}{2}=-\frac{27}{4}+\frac{15}{4}+\frac{2}{4}=-\frac{10}{4}<0\\ f^{\text{'}}\left(0\right) & =& -\frac{3}{4}{\left(0\right)}^2-\frac{5}{4}\left(0\right)+\frac{1}{2}=\frac{1}{2}>0\\ f^{\text{'}}\left(1\right) & =& -\frac{3}{4}{\left(1\right)}^2-\frac{5}{4}\left(1\right)+\frac{1}{2}=-2+\frac{1}{2}<0\end{array}$

Vi kan då setje opp forteiknslinja til $f^{\text{'}}\left(x\right)$.

Vi ser av forteiknslinja at

• Grafen søkk for $$ x\in ⟨\leftarrow , -2⟩$$ og for $$ x\in ⟨\frac{1}{3}, \to ⟩$$.
• Grafen stig for $x\in ⟨-2, \frac{1}{3}⟩$.

Grafen til $f$ har altså eit toppunkt når $x=\frac{1}{3}$ og eit botnpunkt når $x=-2$ .

$\begin{array}{rcl}f\left(-2\right)& = & -\frac{1}{4}{\left(-2\right)}^3-\frac{5}{8}{\left(-2\right)}^2+\frac{1}{2}\left(-2\right)+\frac{3}{8}=\frac{16}{8}-\frac{20}{8}-\frac{8}{8}+\frac{3}{8}=-\frac{9}{8}\\ & & \\ f\left(\frac{1}{3}\right)& =& -\frac{1}{4}{\left(\frac{1}{3}\right)}^3-\frac{5}{8}{\left(\frac{1}{3}\right)}^2+\frac{1}{2}\left(\frac{1}{3}\right)+\frac{3}{8}=-\frac{1}{2^2·3^{{}^3}}-\frac{5}{2^3·3^2}+\frac{1}{2·3}+\frac{3}{2^3}\\ & & \\ & =& \frac{-2-15+36+81}{2^3·3^3}=\frac{100}{2^3·3^3}=\frac{25}{54}\end{array}$

Toppunktet er $\left(\frac{1}{3} , f\left(\frac{1}{3}\right)\right)=\left(\frac{1}{3} , \frac{25}{54}\right)$.
Botnpunktet er $\left(-2 , f\left(-2\right)\right)=\left(-2 ,- \frac{9}{8}\right)$.

Det står no att å finne nullpunkta til $f$ for å ha tilstrekkeleg grunnlag for å teikne ei skisse av grafen.

Funksjonsuttrykket til $f$ er eit tredjegradspolynom. Vi prøver om $x=-1$ kan vere eit nullpunkt for polynomet:

$f\left(-1\right)=-\frac{1}{4}{\left(-1\right)}^3-\frac{5}{8}{\left(-1\right)}^2+\frac{1}{2}\left(-1\right)+\frac{3}{8}=\frac{2}{8}-\frac{5}{8}-\frac{4}{8}+\frac{3}{8}=-\frac{4}{8}\ne 0$

Vi prøver om $x=1$ kan vere eit nullpunkt for polynomet:

$f\left(1\right)=-\frac{1}{4}{\left(1\right)}^3-\frac{5}{8}{\left(1\right)}^2+\frac{1}{2}\left(1\right)+\frac{3}{8}=-\frac{2}{8}-\frac{5}{8}+\frac{4}{8}+\frac{3}{8}=0$

Det betyr $f\left(x\right)$ er deleleg med $x-1$.

Vi gjer polynomdivisjonen:

$\begin{array}{cccccccccccccccccccccccccc}& & -& \frac{1}{4}& x^3& -& \frac{5}{8}& x^2& +& \frac{1}{2}& x& +& \frac{3}{8}& :& (& x& -& 1& )& =& -\frac{1}{4}{x}^2-\frac{7}{8}x-\frac{3}{8}& & & & & \\ -& (& -& \frac{1}{4}& x^3& +& \frac{1}{4}& x^2& )& & & & & & & & & & & & & & & & & \\ & & & & & -& \frac{7}{8}& x^2& +& \frac{1}{2}& x& +& \frac{3}{8}& & & & & & & & & & & & & \\ & & & -& (& -& \frac{7}{8}& x^2& +& \frac{7}{8}& x& )& & & & & & & & & & & & & & \\ & & & & & & & & -& \frac{3}{8}& x& +& \frac{3}{8}& & & & & & & & & & & & & \\ & & & & & & -& (& -& \frac{3}{8}& x& +& \frac{3}{8}& )& & & & & & & & & & & & \\ & & & & & & & & & & & & 0& & & & & & & & & & & & & \end{array}$

No er $f\left(x\right)=\left(-\frac{1}{4}{x}^2-\frac{7}{8}x-\frac{3}{8}\right)\left(x-1\right)$.

Vi løyser så likninga

$\begin{array}{rcl}-\frac{1}{4}{x}^2-\frac{7}{8}x-\frac{3}{8} & =& 0\\ 2x^2+7x+3 & =& 0\\ x & =& \frac{-7\pm \sqrt{49-24}}{4}=\frac{-7\pm 5}{4}\\ x & =& -\frac{1}{2} \mathrm{eller} x=-3\end{array}$

Det betyr at $f\left(x\right)$ har nullpunkta $x=-3, x=-\frac{1}{2} \mathrm{og} x=1.$

På grunnlag av dei opplysningane vi no har, kan vi teikne ei skisse av grafen. Vi teiknar her grafen i GeoGebra:

Ein liten ting til

Dersom ein funksjon er avgrensa på eit lukka intervall, som til dømes $$ \left[-2,3\right]$$, blir ikkje endepunkta rekna som ekstremalpunkt.