Ein sirkel i planet
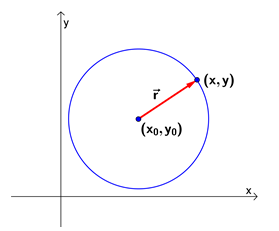
Til høgre ser du ein sirkel med sentrum i punktet. Vi set radius i sirkelen lik . Sirkelen er samlinga av, eller den geometriske staden for, alle punkt som har avstanden frå punktet.
Vi lar vere vektoren frå sentrum i sirkelen,
Då er
Dette gir
Setning
Likninga for ein sirkel med sentrum i
Legg merke til at ein sirkel per definisjon berre er samlinga av punkt som har avstanden r frå sentrum.
Nokre gonger blir likevel omgrepet «sirkel» nytta om heile området som er avgrensa av denne samlinga av punkt. Vi snakkar til dømes om «arealet av ein sirkel». Punkta som har avstanden r frå sentrum, blir då kalla «sirkelperiferien».
Døme 1
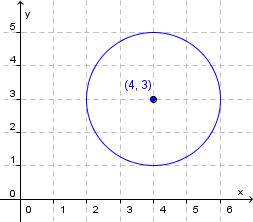
Vi skal finne likninga for ein sirkel som har sentrum i
Her er
Setninga ovanfor gir oss likninga for denne sirkelen
Døme 2
Vi skal bestemme sentrum og radius i ein sirkel som er gitt ved
Om vi samanliknar med likninga
Sirkelen har sentrum i
Ein sirkel har likninga
Vi har sett at likninga for ein sirkel med sentrum i
Vi kan rekne ut venstresida slik:
Vi ser at vi får eit uttrykk der både
Likninga kan derfor vere ei sirkellikning.
For å vere heilt sikre, og finne sentrum og radius i ein eventuell sirkel, må vi skrive om likninga slik at vi får henne på forma
Uttrykka
I matematikk 1T lærte du å skrive om uttrykk for å lage fullstendige kvadrat. Nedanfor har vi teke med to døme, men om du er usikker, kan du gå til sida Faktorisering av andregradsuttrykk ved å lage fullstendige kvadrat frå 1T og repetere dette skikkeleg!
Hugs at eit fullstendig kvadrat er eit andregradsuttrykk som kan faktoriserast ved hjelp av første eller andre kvadratsetning.
Døme 1
Vi skal undersøkje om
Vi må då sjekke om førstegradsleddet er «det dobbelte produktet», det vil seie
Her er
Då er
Døme 2
Vi skal leggje til eit konstantledd slik at uttrykket
Sidan andregradsleddet er
«Det dobbelte produktet»,
Då er
Vi får då at
For å lage fullstendig kvadrat seier vi ofte at vi må «halvere, kvadrere og addere». Ser du kva vi meiner med det? Legg merke til at
Sirkelen vår
No går vi tilbake til sirkelen gitt ved likninga
Vi sorterer ledda og legg til det vi manglar for å få fullstendige kvadrat.
Legg merke til at vi legg til dei same ledda på begge sidene av likskapsteiknet!
Kvifor må vi gjere det?
Dette er altså likninga for ein sirkel med sentrum i