Fagstoff

Pris og etterspørsel

Prisen på ei vare vil påverke kor mange einingar av vara ei bedrift får selt. Korleis kan vi finne prisen som gir størst overskot?

Inntekt og pris

Inntektsfunksjonen

Ei bedrift kan ikkje berre bestemme prisen på ei vare, gå ut frå at alt blir selt, og ut ifrå dette berekne den produksjonen som gir størst overskot. Kanskje prisen er sett så høgt at ikkje alle varene blir selde?

Vi ser på eit døme frå sida Kostnads-, inntekts- og overskotsfunksjon. Klasse 3STB har komme fram til at inntektsfunksjonen $I$ ved sal av treningsapparatet Multiform er gitt ved

$I (x) = 800 x - 2 x^{2}, D_{I} = [0, 150]$

Inntekta ved sal er alltid lik prisen per eining multiplisert med talet på selde einingar. Dersom vi føreset at alle produserte einingar blir selde, er $I (x) = p \cdot x$ , der $x$ er talet på produserte og selde einingar, og $p$ er prisen per eining.

Prisfunksjonen

I dette dømet kan vi komme fram til ein funksjon for prisen $p$ . Ved å faktorisere inntektsfunksjonen får vi at

$I (x) = 800 x - 2 x^{2} = (800 - 2 x) \cdot x$

Det betyr at vi kan sjå på faktoren $(800 - 2 x)$ som prisen på vara, sidan inntekta er pris multiplisert med talet på selde einingar. Prisen blir derfor her ein funksjon av talet på einingar $x$ .

$p (x) = 800 - 2 x, D_{p} = [0, 150]$

Prisfunksjonen er lineær med negativt stigningstal. Vi ønsker å finne verdimengda $V_{p}$ til prisfunksjonen.

$\begin{array}{rcl} p (0) & = & 800 - 2 \cdot 0 = 800 \\ p (150) & = & 800 - 2 \cdot 150 = 500 \end{array}$

Kva blir verdimengda ut ifrå dette?

Verdimengda til prisfunksjonen

Resultata betyr at prisen varierer mellom 800 og 500 kroner. Verdimengda er altså

$V_{p} = [500, 800]$

Aktivitet

Sidan prisen er ein funksjon av talet på einingar, er talet på einingar avhengig av prisen. Endre på likninga $p = 800 - 2 x$ slik at ho blir på forma " $x =$ ".

Løysing

$p = 800 - 2 x \Rightarrow 2 x = 800 - p \Rightarrow x = 400 - 0, 5 p$

Tenk over

Kva betyr dette resultatet i praksis?

Betydning

Det betyr at ifølge denne modellen er det prisen som bestemmer $x$ , det vil seie at prisen bestemmer kor mykje vi får selt, og dermed kor mange einingar vi skal produsere.

Vi vil påpeike at dette er ei grov forenkling av korleis pris og talet på produserte og selde einingar heng saman i verkelegheita. Til vanleg vil vi heller ikkje komme fram til ein samanheng mellom pris og talet på selde einingar ut ifrå inntektsfunksjonen, slik vi har gjort her.

Etterspørselen

$x$ er framleis talet på produserte og selde einingar. Sidan vi føreset at alle einingane blir selde, kan vi kalle talet på einingar for etterspørselen, $e$ , i staden for $x$ . Etterspørselen $e$ er det talet på einingar vi kan forvente å selje når prisen er $p$ . Etterspørselen som funksjon av prisen blir, ut ifrå den omsnudde formelen over,

$e (p) = 400 - 0, 5 p, D_{e} = [500, 800]$

Dette kallar vi for etterspørselsfunksjonen, og denne funksjonen viser kor mange einingar vi kan få selt ved ein bestemd pris. Produksjonen kan då tilpassast salet.

Kostnad og inntekt som funksjon av pris

Når etterspørselen som funksjon av prisen er $e (p) = 400 - 0, 5 p$ , kan både kostnadene og inntekta skrivast som funksjon av prisen. Talet på produserte einingar $x$ blir erstatta direkte av etterspørselen $e$ .

Finn inntektsfunksjonen

Inntektsfunksjonar kan generelt skrivast som $I (x) = p \cdot x$ . Kva blir inntektsfunksjonen $I (p)$ i dømet vårt?

Inntektsfunksjonen I(p)

$\begin{array}{rcl} I (x) & = & p \cdot x \\ I (p) & = & p \cdot e (p) \\ = & p \cdot (400 - 0, 5 p) \\ = & 400 p - 0, 5 p^{2} \end{array}$

Finn kostnadsfunksjonen

Finn kostnadsfunksjonen $K (p)$ ved å erstatte $x$ med $e (p)$ .

Kostnadsfunksjonen K(p)

$\begin{array}{rcl} K (x) & = & 3 x^{2} + 150 x + 11 000 \\ K (p) & = & 3 {(e (p))}^{2} + 150 e (p) + 11 000 \\ = & 3 {(400 - \frac{1}{2} p)}^{2} + 150 (400 - \frac{1}{2} p) + 11 000 \\ = & 3 (160 000 - 2 \cdot 400 \cdot \frac{1}{2} p + \frac{1}{4} p^{2}) + 60 000 - 75 p + 11 000 \\ = & 480 000 - 1 200 p + \frac{3}{4} p^{2} + 60 000 - 75 p + 11 000 \\ = & \frac{3}{4} p^{2} - 1 275 p + 551 000 \end{array}$

Kostnads- og inntektsfunksjonen med CAS

Bruk CAS til å finne $I (p)$ og $K (p)$ ut ifrå etterspørselsfunksjonen $e (p)$ i dømet.

I(p) og K(p) med CAS

Skjermutklipp av CAS-utrekning i GeoGebra. På linje 1 står det e av p kolon er lik 400 minus 0,5 p. Dette blir så gjort om til e av p kolon er lik minus ein halv p pluss 400. På linje 2 står det I av p kolon er lik p e. Resultatet er I av p kolon er lik minus ein halv p i andre pluss 400 p. På linje 3 står det K av p kolon er lik 3 e i andre pluss 150 e pluss 11000. Resultatet er K av p kolon er lik 3 fjerdedels p i andre minus 1275 p pluss 551000.

Overskot som funksjon av pris

Vi viser resten av dømet med bruk av CAS. Overskotsfunksjonen finn vi som før ved å sjå på forskjellen mellom inntekta og kostnadene. Så finn vi det største overskotet som toppunktet til funksjonen.

Overskotsfunksjonen

Bruk CAS, finn overskotsfunksjonen $O (p)$ og den prisen som gir det største overskotet.

Løysing

Skjermutklipp av CAS-utrekning i GeoGebra. På linje 4 står det O av p kolon er lik I minus K. Resultatet er O av p kolon er lik minus 5 fjerdedels p i andre pluss 1675 p minus 551000. På linje 5 står det O derivert av p er lik 0. Svaret med N Løys er p er lik 670.

Sidan overskotsfunksjonen er ein andregradsfunksjon med negativ koeffisient framfor andregradsleddet, veit vi at funksjonen har eit toppunkt. Det største overskotet får elevane derfor når prisen er 670 kroner.

Til slutt reknar vi ut kor stort overskotet blir med denne prisen, og vi må finne ut kor mange einingar (trimapparat) vi skal produsere.

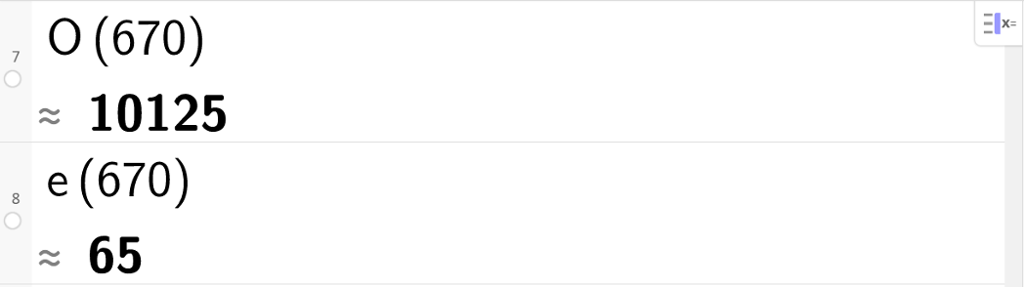
Skjermutklipp av CAS-utrekning i GeoGebra. På linje 7 står det O av 670 er tilnærma lik 10125. På linje 8 står det e av 670 er tilnærma lik 65.

Det maksimale overskotet er på 10 125 kroner per veke. Etterspørselen ved denne prisen er 65 einingar.

Dette er det same talet på einingar som vi har funne på sida Kostnads-, inntekts- og overskotsfunksjon. Det er fordi vi tok utgangspunkt i den opphavlege inntektsfunksjonen $I (x)$ for å komme fram til etterspørselsfunksjonen. I andre situasjonar har vi ingen gitt inntektsfunksjon, berre ein gitt etterspørselsfunksjon.

Grafisk løysing

Vi får det same resultatet grafisk.

Illustrasjon av eit koordinatsystem. X-aksen viser p, pris per eining i kroner, og har verdiar frå 0 til 1300. Y-aksen går frå 0 til 100000 og har eininga kroner. I av p og K av p er teikna inn. O av p er også teikna inn, og denne grafen har eit toppunkt med koordinatar 670 og 10125.

Vi kan i tillegg finne kva prisar vi må halde oss innanfor dersom vi skal gå med overskot. Då kan vi til dømes finne nullpunkta til overskotsfunksjonen $O$ .

Tenk over

I utgangspunktet hadde elevane tenkt å selje treningsapparatet til 800 kroner. Kva betyr det at den prisen som gir størst overskot, er 670 kroner?

Betydning av resultat

Elevane hadde komme fram til at dersom dei skulle selje mykje, ville dei ikkje kunne få like mykje for alle apparata fordi dei ikkje kunne ta den same prisen ved sal til sportsbutikkar. Prisen på 670 kroner kan vi derfor tolke som ein slags gjennomsnittspris på dei 65 treningsapparata.

Funksjonsanalyse og modellering

Inntekt og pris

Inntektsfunksjonen

Prisfunksjonen

Aktivitet

Tenk over

Etterspørselen

Kostnad og inntekt som funksjon av pris

Finn inntektsfunksjonen

Finn kostnadsfunksjonen

Kostnads- og inntektsfunksjonen med CAS

Overskot som funksjon av pris

Overskotsfunksjonen

Grafisk løysing

Tenk over