Grensekostnad og grenseinntekt
Grensekostnad, definisjon
Grensekostnaden er kostnaden ved å produsere éi ekstra eining av ei vare ved ei gitt produksjonsmengde.
Kostnadsfunksjon, grensekostnad og momentan vekstfart
Vi går ut ifrå at vi har ein kostnadsfunksjon å ta utgangspunkt i. Grensekostnaden når produksjonen til dømes ligg på 1 000 einingar, det vil seie endringa i kostnadene ved å auke produksjonen frå 1 000 til 1 001, kan vi rekne ut med
Vi kan omformulere definisjonen av grensekostnaden til å vere kor mykje kostnaden endrar seg per eining ved ei gitt produksjonsmengde. Dette er det same som den momentane vekstfarten til kostnadsfunksjonen i dette punktet.
Døme: elevbedrift
Vi skal prøve dette på dømet med elevbedrifta som skal produsere treningsapparatet Multiform, sjå sida Kostnads-, inntekts- og overskotsfunksjon.
Elevane i elevbedrifta har komme fram til kostnadsfunksjonen
Vi ønsker å finne grensekostnaden når produksjonen er på 20 einingar og på 100 einingar. På figuren nedanfor har vi teikna kostnadsfunksjonen i det aktuelle området saman med dei to punkta på grafen der
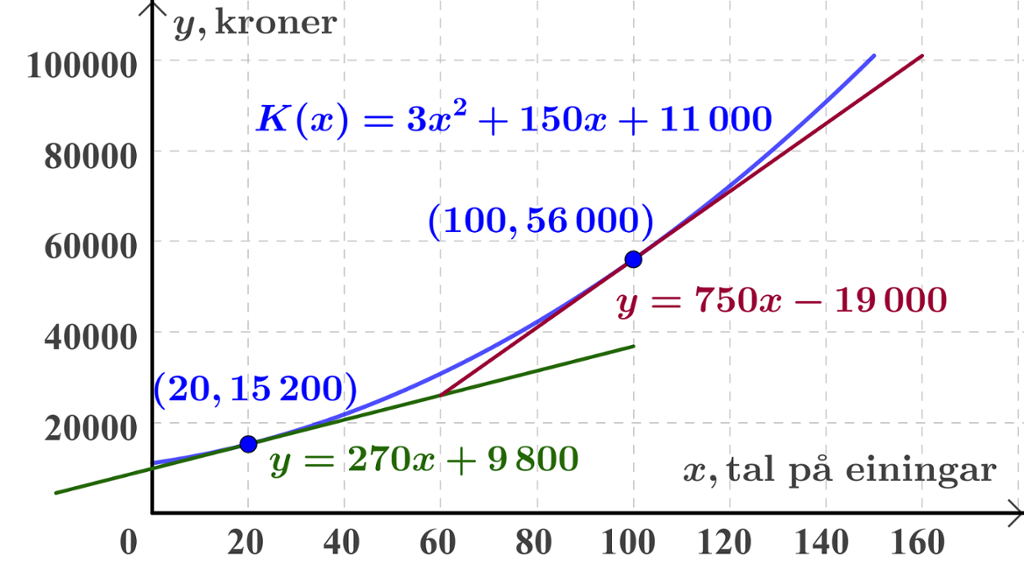
Vi kan no finne frå stigningstalet til tangenten at den momentane vekstfarten til kostnadsfunksjonen når
Kva betyr eigentleg dette?
Tenk over korleis vi kan finne grensekostnaden ved 20 produserte einingar ved rekning. I boksen nedanfor ser du korleis vi har gjort det.
Vis ved rekning at grensekostnaden når
Bruk figuren og finn grensekostnaden i dømet når elevbedrifta produserer 100 einingar. Rekn deretter ut det same ved å bruke
Tenk over kva grunnar det kan vere til at grensekostnaden når
Grensekostnad, definisjon og oppsummering
Grensekostnaden er endringa i kostnadene ved å produsere éi ekstra eining av ei vare ved ei gitt produksjonsmengde.
Vi kan finne grensekostnaden i eit punkt ved å finne den momentane vekstfarten til kostnadsfunksjonen i punktet.
Ofte kallar vi berre den deriverte av kostnadsfunksjonen,
Grenseinntekt blir definert tilsvarande som grensekostnad.
Grenseinntekt, definisjon og oppsummering
Grenseinntekta er endringa i inntektene ved å selje éi ekstra eining av ei vare ved ei gitt mengde selde einingar.
Vi kan finne grenseinntekta i eit punkt ved å finne den momentane vekstfarten til inntektsfunksjonen i punktet.
Ofte kallar vi berre den deriverte av inntektsfunksjonen,
Grenseinntekt for elevbedrifta
Elevbedrifta som sel treningsapparatet Multiform, har komme fram til at inntektsfunksjonen
Vi ønsker å finne grenseinntekta ved 20 selde einingar. Det kan vi gjere ved å derivere inntektsfunksjonen og rekne ut
Grenseinntekta ved 20 selde einingar er 720 kroner. Det betyr at elevane forventar at inntekta aukar med 720 kroner dersom dei sel eitt treningsapparat ekstra når produksjonen ligg på 20 einingar i veka.
Prøv sjølv: Finn grenseinntekta ved 100 selde einingar.
Samanlikn dei to tala for grenseinntekta.
Vi fekk frå avsnitta over at
K ' 20 = 270 , I ' 20 = 720 K ' 100 = 750 , I ' 100 = 400
Vi får at når produksjonen ligg på 20 einingar per veke, kostar det 270 kroner å produsere éi eining ekstra. Men samtidig aukar inntekta med 720 kroner. Det betyr at overskotet aukar, så det vil lønne seg å auke produksjonen – dersom ein går ut frå at dei får selt alle 21 apparata.
Kva skjer med overskotet dersom produksjon (og sal) ligg på 100 einingar og elevbedrifta ønsker å auke produksjonen?
Kva kan vi konkludere ut ifrå dette?
Den deriverte av overskotsfunksjonen
Vi kan vise at konklusjonen vi kom fram til over, gjeld generelt.
Vi har frå teorisida om kostnads-, inntekts- og overskotsfunksjonar at det største moglege overskotet ei bedrift kan ha, er der overskotsfunksjonen har den største verdien sin. Som regel finn vi denne verdien i eit toppunkt der den deriverte er lik 0. Vi kan sjå for oss situasjonar der det største overskotet finst anten i eit endepunkt eller i eit knekkpunkt, men desse situasjonane er spesialtilfelle.
Vi har generelt at
Vi prøver å derivere det generelle uttrykket for overskotsfunksjonen:
Kva får vi dersom vi set den deriverte,
Vilkår for størst mogleg overskot
Det største moglege overskotet er der kvar den deriverte av inntektsfunksjonen er lik den deriverte av kostnadsfunksjonen.
Vi kan òg seie at det største moglege overskotet er der grensekostnaden er lik grenseinntekta.
I tillegg må vi sjekke om maksimalverdien til overskotsfunksjonen kan ligge i nokon av endepunkta til funksjonen eller i eit knekkpunkt der den deriverte ikkje eksisterer.