Modellar av figurar og mønster
Figurane ovanfor er bygde opp av 9, 12 og 15 små kvadrat. Tenk deg at vi held fram å lage figurar etter same mønster.
Talet på små kvadrat i kvar figur dannar ein serie med tal, ei talfølgje, som byrjar med tala 9, 12 og 15 og held fram etter same mønster i det uendelege 9, 12, 15, ...
La vere talet på små kvadrat i figur nummer slik at og
Prøv å svare på desse spørsmåla før du ser på løysinga.
- Kva gjer vi for å komme frå éin figur til den neste? Kva er mønsteret i det vi gjer?
- Kor mange små kvadrat vil det vere i Figur 4, Figur 5 og Figur 6? Det vil seie og F6.
- Kan du finne ein modell, ein formel, for talet på kvadrat i figur nummer ? Ein formel for .
- Kor mange kvadrat er det etter din modell i figur nummer 998?
Løysning
Ein likesida har areal lik . Midtpunkta på sidene i er hjørna i ein ny likesida trekant med areal lik . Midtpunkta på sidene i er hjørna i ein ny likesida trekant med areal lik . Etter same mønster lager vi trekanter med areal , og så vidare.
Denne prosessen tenkjer vi oss held fram i det uendelege. Sjå skissa nedanfor.
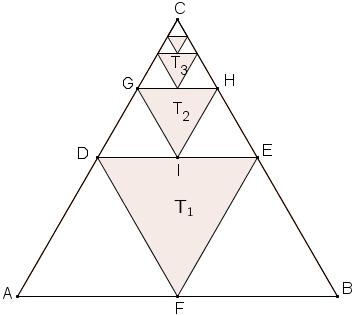
Oppgåve
- Kva blir arealet til trekant ? Kva blir arealet til trekant ? Kva blir arealet til trekant ?
- Kan du finne ein modell, ein formel, for arealet når vi held frem å lage trekantar etter same mønster?
- Bruk modellen, og set opp eit uttrykk for arealet ? Kva blir arealet ?
- Studer figuren og finn ut kva som blir summen av areala , og så videre. Omkrinsen av er lik 3. Trekanten som har arealet lik har omkrinsen .
- Forklar at .
- Kan du finne en modell, en formel, for omkrinsen til trekant nr. når vi held fram å lage trekantar etter same mønster?
- Bruk modellen og finn .
Løysing