Gjennomsnittleg og momentan vekstfart
Døme på gjennomsnittleg vekstfart: kroppshøgde

Som 13-åring var Nils Henrik 149 cm høg. Då han var 17, var han 181 cm. Kor mykje vaks Nils Henrik i denne perioden i gjennomsnitt per år?
Gjennomsnittleg vekstfart – grunnleggande definisjon
Den gjennomsnittlege vekstfarten seier kor mykje ein storleik
Tenk over
Kan vi finne ut kor høg Nils Henrik var då han var 14 år?
Kva har vi brukt som føresetnad i utrekninga i boksen over?
I dømet over er storleiken
Gjennomsnittleg vekstfart grafisk
Vi skal no sjå korleis gjennomsnittleg vekstfart ser ut grafisk.
Teikn informasjonen om alderen til Nils Henrik som to punkt i eit koordinatsystem der vi har alderen målt i år på
Øvst på sida rekna vi ut den gjennomsnittlege vekstfarten med reknestykket
Vi finn òg igjen tala i reknestykket i koordinatsystemet i boksen over. Kvar?
Vi teiknar ei linje igjennom dei to punkta, sjå figuren. Det vassrette, stipla linjestykket har lengde
Tilsvarende har det loddrette linjestykket lengde
Det betyr at den gjennomsnittlege vekstfarten kan uttrykkast som
Tenk over
Studer figuren over. Kva betydning har forholdet
På figuren har vi teikna linja ved hjelp av kommandoen "Linje" eller den tilsvarande verktøyknappen. Så har vi brukt kommandoen (eller verktøyknappen) "Stigning" for å finne at stigningstalet til linja er 8.
Gjennomsnittleg vekstfart mellom to punkt
Den gjennomsnittlege vekstfarten frå eit punkt
Gjennomsnittleg vekstfart til ein funksjon
No går vi ut frå at høgda
der
Gjennomsnittleg vekstfart til ein funksjon oppsummert
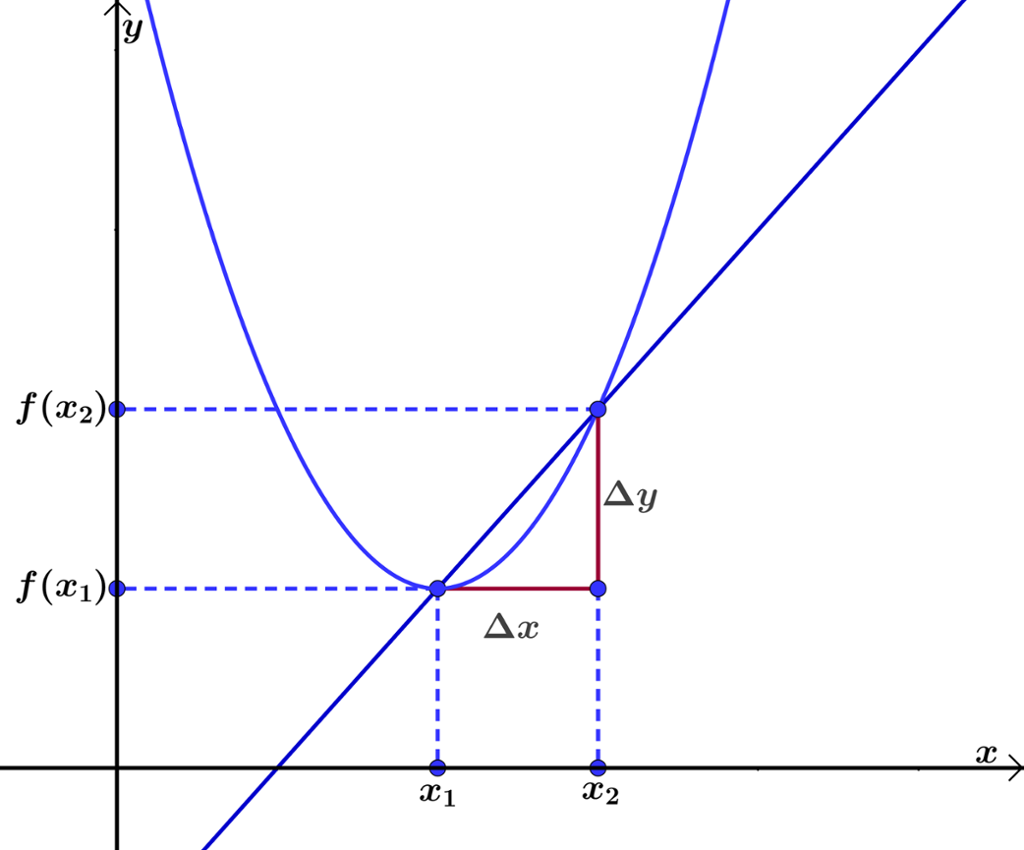
Den gjennomsnittlege vekstfarten for ein funksjon
Ein sekant er ei rett linje som skjer ei krum kurve i minimum to punkt.
Vi går framleis ut frå at høgda til Nils Henrik følger funksjonen
Tenk over
Vi såg i dømet over at Nils Henrik vaks i gjennomsnitt 8 cm per år frå han var 13 til han var 17. Kan du ut frå grafen seie noko om når i denne perioden han vaks raskast?
Kor raskt vaks han eigenleg per år akkurat då? For å svare på det kan du bruke GeoGebra-simuleringa nedanfor, der du kan dra i den svarte glidaren for å flytte på punktet til høgre og observere endringa i stigningstalet til linja. Dersom simuleringa ikkje blir vist, kan du laste ho ned nedanfor.
Når vi flyttar det svarte punktet til det overlappar det blå, får vi at stigningstalet til linja blir 12. Det betyr at då Nils Henrik var 13 år, vaks han med ein fart av 12 cm per år. Merk at dette gjeld berre då han var 13 år, eller når
Når dei to punkta overlappar, er ikkje linja lenger ein sekant som skjer grafen i to punkt, men ein tangent til grafen i punktet
Momentan vekstfart, definisjon
Den momentane vekstfarten til ein funksjon i eit punkt på grafen er stigningstalet til tangenten til grafen i dette punktet.
Merk òg at både gjennomsnittleg og momentan vekstfart får måleininga cm/år eller cm per år, altså måleininga på
Vi kan bruke den momentane vekstfarten til ein funksjon som ei tilnærming til kor mykje funksjonen veks når
Vi skal vise korleis vi finn den momentane vekstfarten til funksjonen (og Nils Henrik) når
Momentan vekstfart grafisk
Vi har følgt oppskrifta nedanfor då vi laga biletet i boksen over, bortsett frå at vi teikna tangenten i punktet
Vi teiknar funksjonen ved å skrive han inn i algebrafeltet.
Vi teiknar punktet
14 , h 14 Vi teiknar tangenten til grafen i punktet ved å velje verktøyet "Tangentar", sjå biletet, klikke på punktet og deretter klikke ein stad på grafen til
h Vi finn stigningstalet til tangenten ved å velje verktøyet "Stigning" og klikke på tangentlinja. Dette stigningstalet er den momentane vekstfarten til grafen i punktet
14 , h 14
Ved å følge desse punkta skal du få at stigningstalet til tangenten er 10. Den momentane vekstfarten til funksjonen når
Momentan vekstfart med CAS
Vi finn den momentane vekstfarten med CAS enklast på denne måten:
Skriv inn funksjonen i CAS.
Vi kombinerer kommandoane "Stigning" og "Tangent" ved å setje tangentkommandoen saman med den aktuelle
x
Kommentar: Vi kan òg finne tangenten først og deretter bruke kommandoen "Stigning" dersom vi føretrekker å gjere det på to linjer. Eit tredje alternativ er å berre bruke kommandoen "Tangent". Det kan vi gjere sidan vi kan lese ut stigningstalet direkte frå likninga til tangenten.