Meir om stigingstalet
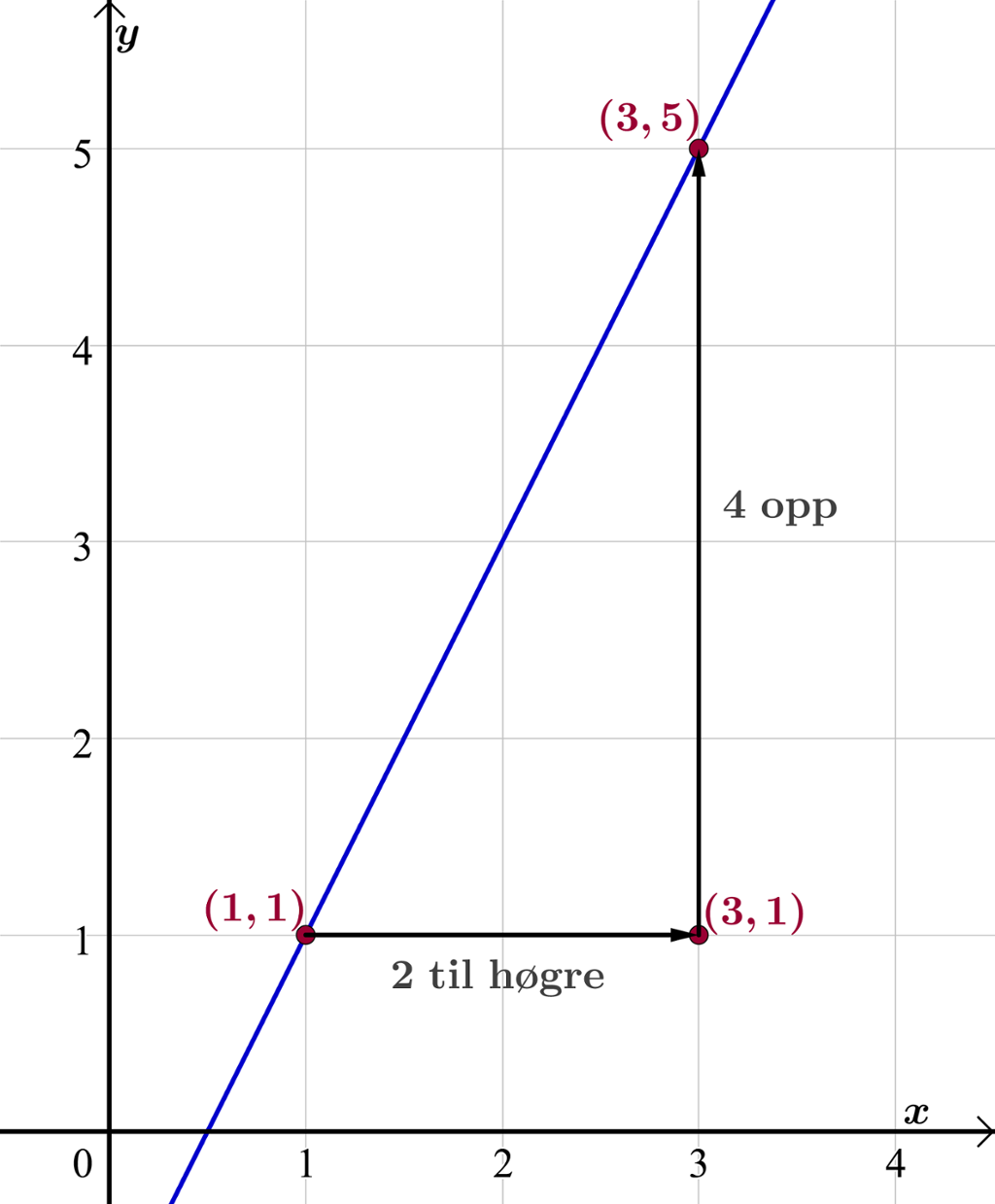
Tidligare fann vi stigingstalet til den gitte grafen ved å starte i eit punkt på grafen og så gå éi eining til høgre.
Ved å starte i punktet og til dømes gå to einingar til høgre, må vi gå fire einingar oppover parallelt med -aksen for igjen å treffe grafen. Stigingstalet blir
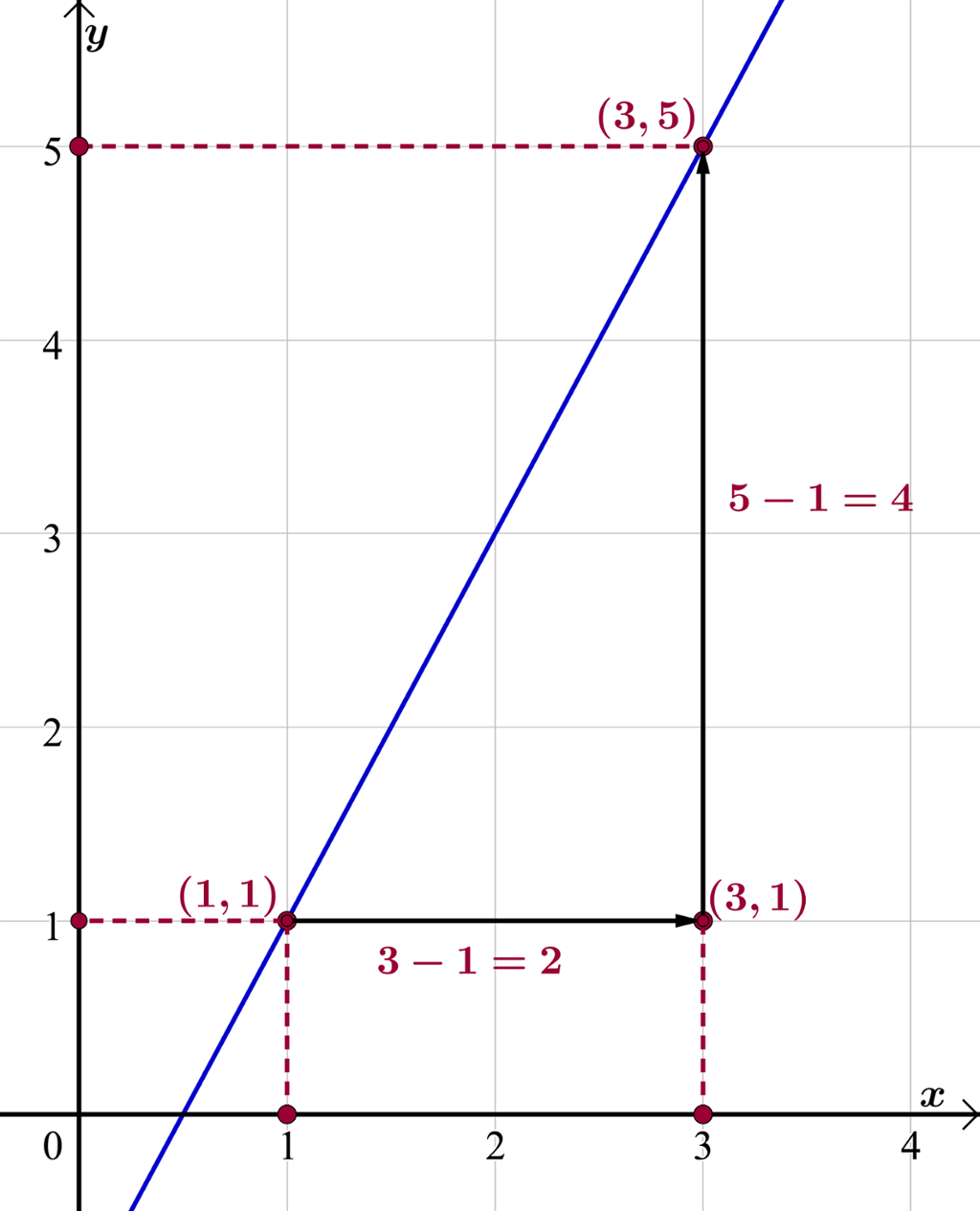
Dette kan vi også rekne oss fram til med utgangspunkt i dei to punkta på grafen
I teljaren har vi endring i -verdi og i nemnaren endring i -verdi.
Endring i -verdi dividert med endring i -verdi gir alltid verdien for stigingstalet fordi stigingstalet er endring i -retning per enhet på -aksen
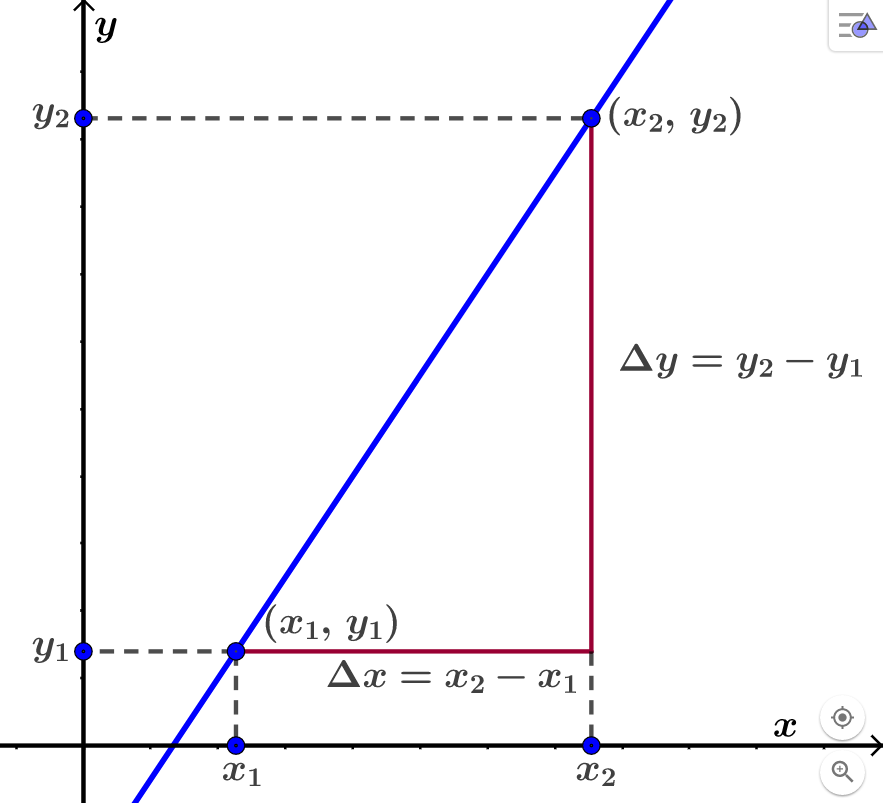
Vi let no og vere to vilkårlege punkt på linja. Legg merke til korleis vi brukar indeksar, 1 og 2, for å «namngi» punkt 1 og punkt 2.
Det er vanleg å la den greske bokstaven delta, , stå for endring.
Vi let vere endring i -verdi og vere endring i -verdi.
Stigingstalet til linja blir