Bruk av formlikhet for å regne ut ukjente sider i trekanter
Trekantene og er formlike. Regn ut lengdene til de ukjente sidene.
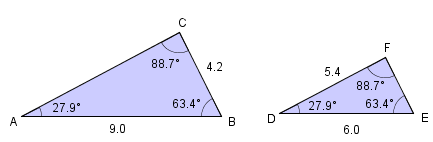
Her ser vi at sidene og er tilsvarende sider fordi begge er motstående sider til vinklene på . Sidene og ligger begge motsatt av vinklene som er og er også tilsvarende. Det samme er sidene og .
Vi kan finne de ukjente sidene ved å bruke målestokken.
Vi regner ut målestokken når vi går fra til . Målestokken er
Det betyr at
.
Når vi går motsatt vei, må vi dele med målestokken. Det betyr at
Et tre står på en horisontal slette. Vi skal finne ut hvor høyt treet er uten å felle det.
Utstyr: Sol og metermål
Vi setter en pinne ned i bakken litt bortenfor treet og måler avstanden skyggen kaster ved pinnen og ved treet. Se figuren nedenfor.
Både pinnen og treet danner en vinkel på 90° med bakken, og solstrålene danner samme vinkel med bakken der hvor pinnen står som der hvor treet står. Vi får derfor to formlike trekanter, og det fremgår av figuren hvilke sider som er tilsvarende.
Vi regner ut målestokken når vi går fra den minste trekanten til den største trekanten
Legg merke til at vi også kan finne den ukjente siden ved å bruke likning.
Vi setter høyden av treet lik , og siden forholdet mellom tilsvarende sider er konstant, kan vi sette opp og løse likningen
Treet er meter høyt.
Spørsmål
Løsningsmetoden vår stiller krav til terrenget der treet står. Hvilket krav er det?
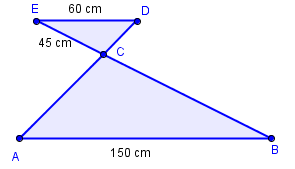
På figuren er og parallelle. Linjestykkene og skjærer hverandre i .
Oppgave
Vis at og er formlike, og bruk dette til å regne ut lengden til siden .
Løsning
siden disse er toppvinkler. Da er sidene og tilsvarende sider.
fordi venstre vinkelbein er felles og høyre vinkelbein er parallelle i de to vinklene. (Samsvarende vinkler ved parallelle vinkelbein).
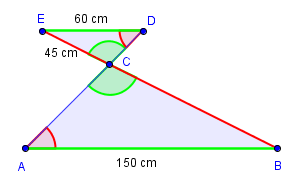
Sidene og er da tilsvarende sider fordi de er motstående sider til like store vinkler.
Vinklene i de to trekantene er parvis like store, og trekantene er formlike.
Vi regner ut målestokken når vi går fra den minste trekanten til den største.
Da er
Også her kan vi løse oppgaven ved å sette opp og løse en likning siden forholdet mellom tilsvarende sider er konstant. Det er lurt å alltid begynne med den ukjente siden.
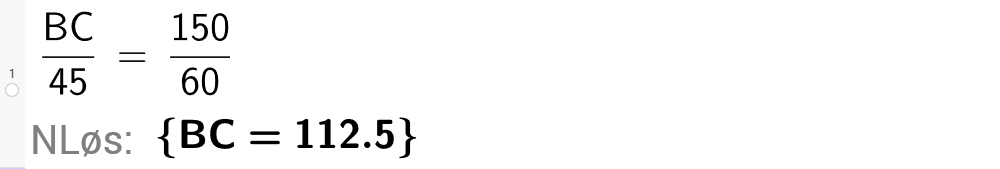
Likningen kan vi også løse med CAS i GeoGebra, se figuren.