Vinkelsummen i en n-kant

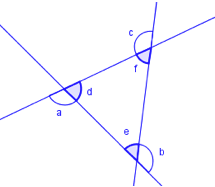
Tenk deg at du spaserer én runde langs linjestykkene på yttersiden av en trekant. Når du går fra ett linjestykke til et annet, endrer du retning slik som vinklene ɑ, b og c på figuren viser. Til sammen endrer du retning 360°. Det vil si at

$a+b+c=360°$

Summen av vinklene i trekanten er $d+e+f$.

$\begin{array}{rcl}d+e+f& = & (180°-a)+(180°-b)+(180°-c)\\ & & \\ & =& 3·180°-(a+b+c)\\ & & \\ & =& 3·180°-(360°)\\ & & \\ & =& 3·180°-2·180°\\ & & \\ & =& (3-2)·180°=180°\end{array}$

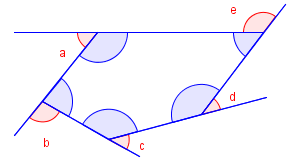
Nå gjør vi det samme med en femkant. Tenk deg at du spaserer én runde langs linjestykkene på yttersiden av en femkant. Når du går fra ett linjestykke til et annet, endrer du retning slik som vinklene ɑ, b, c, d og e på figuren til høyre viser. Til sammen endrer du retning 360°. Det vil si at

$a+b+c+d+e=360°$

Da kan vi regne ut summen av vinklene i femkanten

$\begin{array}{rcl}\mathrm{Vinkelsummen}& = & \left(180°-a\right)+\left(180°-b\right)+\left(180°-c\right)+\left(180°-d\right)+\left(180°-e\right)\\ & & \\ & = & 5·180°-\left(a+b+c+d+e\right)\\ & & \\ & =& 5·180°-\left(360°\right)\\ & & \\ & =& 3·180°+2·180°-360°\\ & & \\ & =& 3·180°\\ & & \\ & =& \left(5-2\right)·180°=540°\end{array}$

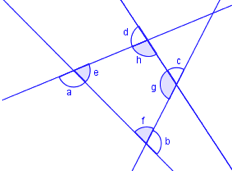
Prøv selv, bruk figuren, før tilsvarende bevis som for vinkelsummen i en trekant og en femkant, og overbevis deg selv om at setningen nedenfor må være riktig.

Vi fikk også et annet resultat av utregningene.

• Vinkelsummen i en 3-kant er $\left(3-2\right)·180°=1·180°=180°$
  
• Vinkelsummen i en 4-kant er $\left(4-2\right)·180°=2·180°=360°$
  
• Vinkelsummen i en 5-kant er $\left(5-2\right)·180°=3·180°=540°$
  

Vi kan gjøre tilsvarende resonnement for alle mangekanter.