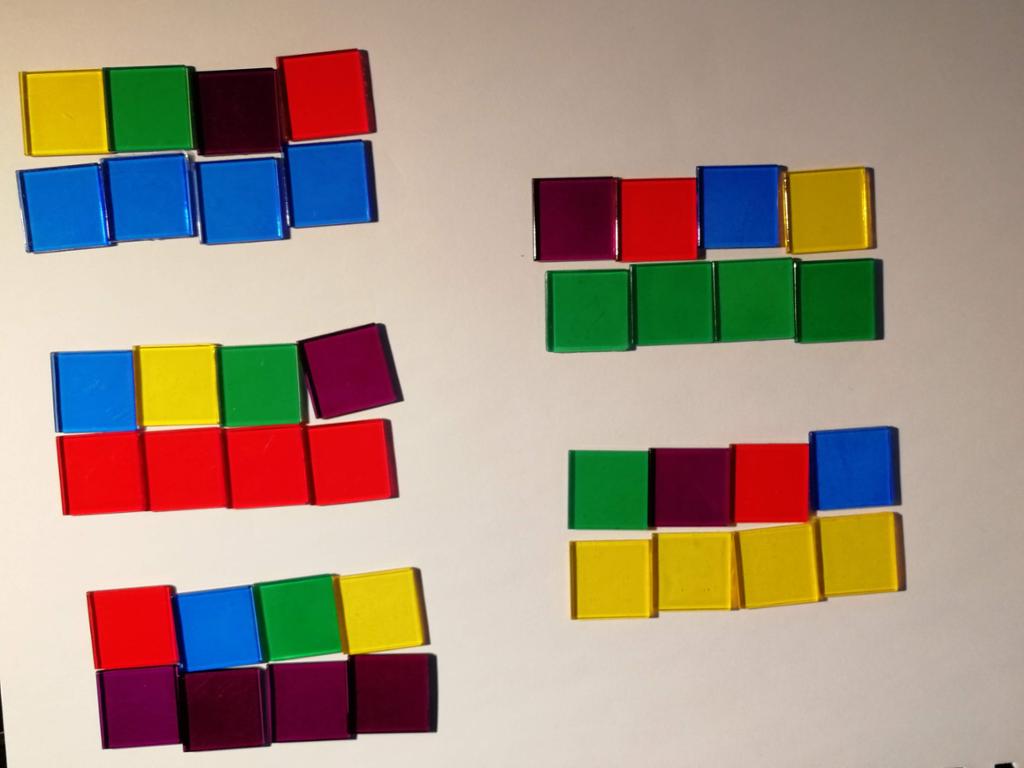Introduksjon til kombinatorikk

Kombinatorikk er en gren innen matematikk vi kan bruke til å finne ut på hvor mange ulike måter vi kan kombinere elementer etter ulike kriterier. Enkelt sagt er kombinatorikk opptelling av hvor mange ulike utfall vi kan få i et forsøk.

Som en introduksjon til kombinatorikk ønsker vi å gjøre en liten øvelse. Dersom skolen din har tellebrikker i ulike farger, kan de være en god hjelp. Hvis ikke du har slike brikker for hånden, kan du tegne med ulike farger eller skrive ulike symboler.

For å gjøre denne øvelsen trenger du brikker i fem forskjellige farger. Du bør ha omtrent 10–15 av hver farge.

Nå skal du prøve å finne ut hvor mange ulike par du kan lage med to av disse fem fargene. Slå deg gjerne sammen med en medelev, og prøv dere fram. Er dere enige om hvilke kriterier dere skal bruke? Får dere ulike svar? Er noen av disse svarene riktigere enn de andre?

Vent gjerne en stund med å åpne tipsboksen under – i den finner du noe å tenke nærmere gjennom.

Løsning nummer 1

Først ser vi på hvordan vi kan få 25 til svar. På bildet under har vi laget fem grupper hvor vi har fem ulike par i hver gruppe, det vil si at vi har 25 par. Vi ser at vi har med par hvor de to brikkene har lik farge, og vi har også med kombinasjonen av for eksempel blå og grønn to ganger. Dette er én måte å lage par med to brikker på når vi har brikker med fem ulike farger å velge blant.

Vi kan observere at vi kunne ha funnet det ut ved regning ved å tenke at vi har fem muligheter for første brikke, og for hver av disse mulighetene har vi fem muligheter, altså $$ 5·5$$ muligheter.

Løsning nummer 2

I løsning nummer 1 så vi at vi hadde med løsninger der de to brikkene var like. Vi kan jo tenke oss en situasjon der det ikke er mulig å ha to like, for eksempel hvis vi bare har en av hver brikke. Hvis vi nå tar vekk alle de parene med to like brikker, sitter vi igjen med fem grupper med fire par i hver gruppe, altså $$ 5·4=20$$ par.

Uten å bruke brikkene og lage figurene kunne vi ha tenkt som i løsning nummer 1: Vi har fem muligheter for brikke nummer 1, men nå bare fire muligheter for brikke nummer 2.

Løsning nummer 3

Hvis vi kikker nøye på løsning nummer 2, ser vi at alle fargekombinasjonene forekommer to ganger. Noen ganger kan rekkefølgen på tellebrikkene ha noe å si. Vi kan for eksempel lage et kodespråk der rød-blå betyr noe annet enn blå-rød. Vi kan også tenke oss situasjoner der det ikke har noe å si hvilken rekkefølge vi legger tellebrikkene i, og at det eneste som betyr noe, er om vi har for eksempel en rød og en blå eller en gul og en grønn brikke. I det siste tilfellet kan vi fjerne halvparten av parene, og vi sitter igjen med $$ \frac{5·4}{2}=10$$ par som på bildet under.

Løsning nummer 4

Vi kan også tenke oss at vi ønsker oss bare par der ingen av parene kan forveksles med hverandre (altså vil vi ikke ha med for eksempel både rød-blå og blå-rød), men vi kan gjerne ha med de parene der begge brikkene er like. Da kan vi legge disse parene tilbake igjen, og vi får 15 par som på bildet under.

Vi sa innledningsvis at kombinatorikk handler om å telle opp antall utfall i et forsøk. Vi kan se på øvelsen med tellebrikkene som et forsøk med fem tellebrikker i fem ulike farger i en hatt. Vi trekker to tellebrikker fra hatten på den måten at vi trekker én og én brikke.

Antall forskjellige utfall vi får i forsøket, avhenger av to ting:

• Legger vi tilbake den første brikken før vi trekker brikke nummer to? Hvis vi gjør det, er to like brikker et mulig utfall. Uten tilbakelegging har vi ikke denne muligheten.
• Skal vi oppfatte for eksempel blå brikke i første trekk og rød brikke i andre trekk som det samme utfallet som rød brikke i første trekk og blå brikke i andre trekk? Sagt på en enklere måte: Skal rekkefølgen bety noe? Hvis rekkefølgen betyr noe, har vi et ordnet utvalg, ellers er det et uordnet utvalg.

I løsning nummer 1 har vi ordnet utvalg med tilbakelegging. Vi får et utvalg med 25 ulike utfall.

I løsning nummer 2 har vi ordnet utvalg uten tilbakelegging. Vi får et utvalg med 20 ulike utfall. De fem mulige utfallene med like brikker forsvinner.

I løsning nummer 3 har vi uordnet utvalg uten tilbakelegging. Vi halverer antall utfall i forhold til løsning nummer 2, siden rekkefølgen ikke betyr noe, og vi ender på 10 utfall. Rød pluss blå er samme utfall som blå pluss rød.

I løsning nummer 4 har vi uordnet utvalg med tilbakelegging. Vi tar med de fem utfallene med like brikker igjen, og vi får fem flere utfall enn i løsning nummer 3.

De tre første typene av utvalg skal du få bli godt kjent med i artikkelen "Tre ulike typer utvalg", men før vi kommer så langt, skal vi jobbe litt med fakultet og binomialformelen.