Bargobihttá

Ulikheter av andre grad

Oppgavene nedenfor skal løses uten bruk av hjelpemidler. Du kan også prøve å løse oppgavene med CAS.

1.10.10

Løs ulikhetene.

vis fasit

Denne ulikheten er ferdig ordna. Vi finner først nullpunktene til uttrykket på venstre side:

Vi vet nå at uttrykket $²$ er lik 0 når og når . Det er bare for disse verdiene av at uttrykket kan skifte fortegn. Vi tar stikkprøver for -verdier i intervallene , og .

Vi bruker det faktoriserte uttrykket når vi tar stikkprøvene.

$å å å$

Vi kan da sette opp fortegnslinjen:

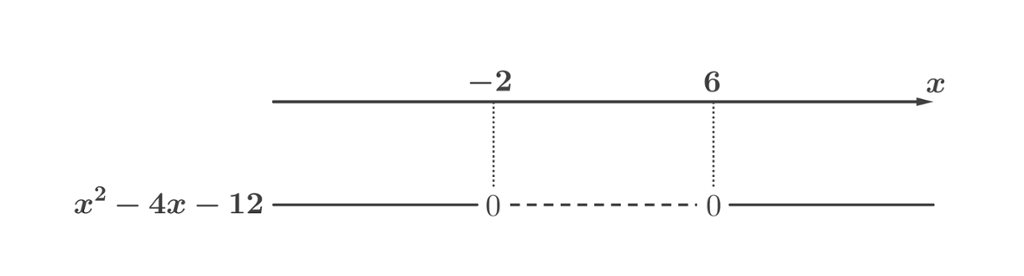
Fortegnslinje for uttrykket x i andre minus 4 x minus 12 som viser at uttrykket er positivt fra minus uendelig til minus 2, negativt fra -2 til 6 og positivt fra 6 til pluss uendelig. Utklipp.

Oppgaven vår var å finne ut for hvilke verdier av det stemte at $²$ . Av fortegnslinjen kan vi lese at ulikheten har løsningen .

Løsning med CAS:

CAS-løsning av ulikheten x i andre minus 4 x minus 12 mindre enn 0. Utklipp.

vis fasit

Vi finner først nullpunktene:

Vi vet nå at uttrykket $²$ er lik 0 når og når $¼$ . Det er bare for disse verdiene av at uttrykket kan skifte fortegn. Vi tar stikkprøver for -verdier i intervallene og .

Vi bruker det faktoriserte uttrykket når vi tar stikkprøvene.

$å å å$

Vi kan da sette opp fortegnslinjen:

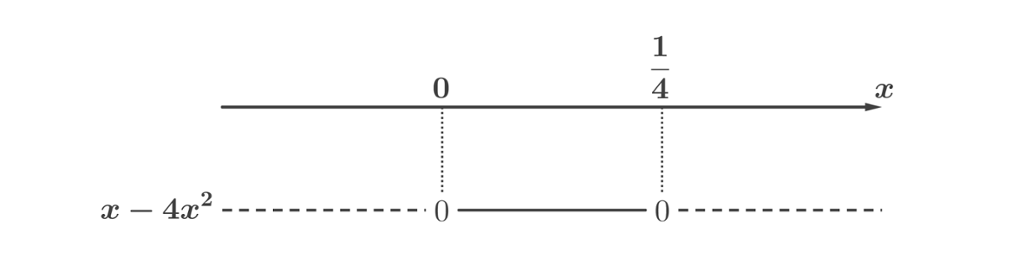
Fortegnslinje for uttrykket x minus 4 x i andre som viser at uttrykket er negativt fra minus uendelig til 0, positivt fra 0 til en fjerdedel og negativt fra en fjerdedel til pluss uendelig. Utklipp.

Oppgaven vår var å finne ut for hvilke verdier av det stemte at $²$ . Av fortegnslinjen kan vi lese at ulikheten har løsningen .

Løsning med CAS:

CAS-løsning av ulikheten x minus 4 x i andre større enn 0. Utklipp.

vis fasit

Vi finner først nullpunktene:

Vi vet nå at uttrykket $²$ er lik når og når $½$ . Det er bare for disse verdiene av at uttrykket kan skifte fortegn. Vi tar stikkprøver for -verdier i intervallene , $½$ , og .

Vi bruker det faktoriserte uttrykket når vi tar stikkprøvene.

$å å å$

Vi kan da sette opp fortegnslinjen:

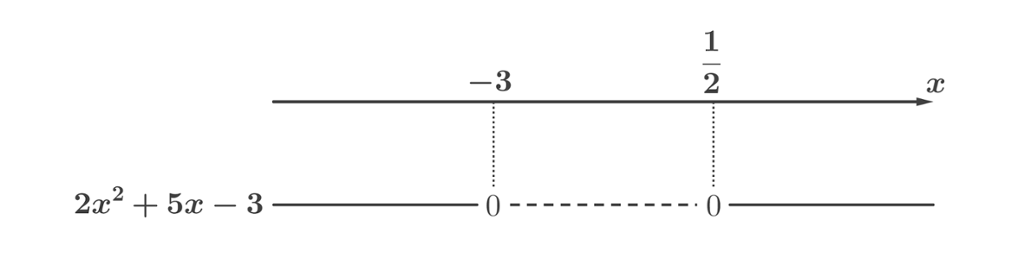
Fortegnslinje for uttrykket 2 x i andre pluss 5 x minus 3 som viser at uttrykket er positivt fra minus uendelig til minus 3, negativt fra minus 3 til en halv og positivt fra en halv til pluss uendelig. Utklipp.

Oppgaven vår var å finne ut for hvilke verdier av det stemte at $²$ . Av fortegnslinjen kan vi lese at ulikheten har løsningen .

Løsning med CAS:

CAS-løsning av ulikheten 2 x i andre pluss 5 x minus 3 større enn eller lik 0. Utklipp.

vis fasit

Vi finner først nullpunktene:

Vi vet nå at uttrykket $²$ er lik 0 når og når . Det er bare for disse verdiene av at uttrykket kan skifte fortegn. Vi tar stikkprøver for -verdier i intervallene og .

Vi bruker det faktoriserte uttrykket når vi tar stikkprøvene.

$å å å$

Vi kan da sette opp fortegnslinjen:

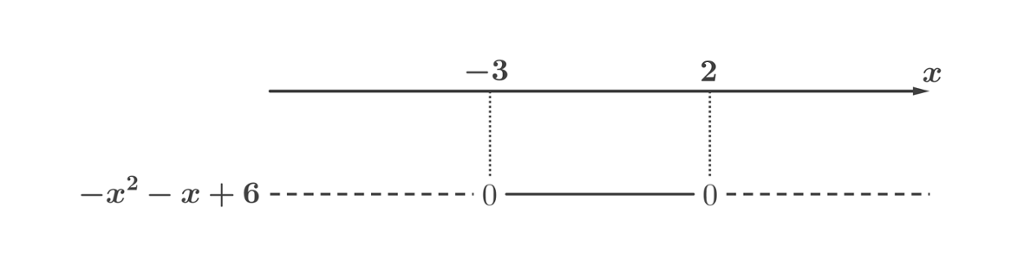
Fortegnslinje for uttrykket minus x i andre minus x pluss 6 som viser at uttrykket er negativt fra minus uendelig til minus 3, positivt fra minus 3 til 2 og negativt fra 2 til pluss uendelig. Utklipp.

Oppgaven vår var å finne ut for hvilke verdier av det stemte at $²$ . Av fortegnslinjen kan vi lese at ulikheten har løsningen .

Løsning med CAS:

CAS-løsning av ulikheten minus x i andre minus x pluss 6 mindre enn eller lik 0. Utklipp.

vis fasit

Vi faktoriserer først uttrykket

Vi vet nå at uttrykket $²$ er lik 0 når og når . Det er bare for disse verdiene av at uttrykket kan skifte fortegn. Vi tar stikkprøver for -verdier i intervallene og .

Vi bruker det faktoriserte uttrykket når vi tar stikkprøvene.

$å å å$

Vi kan da sette opp fortegnslinjen:

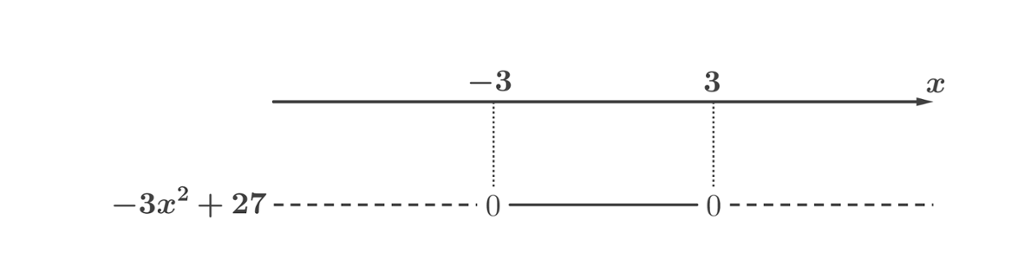
Fortegnslinje for uttrykket minus 3 x i andre pluss 27 som viser at uttrykket er negativt fra minus uendelig til minus 3, positivt fra minus 3 til 3 og negativt fra 3 til pluss uendelig. Utklipp.

Oppgaven vår var å finne ut for hvilke verdier av det stemte at $²$ . Av fortegnslinjen kan vi lese at ulikheten har løsningen .

Løsning med CAS:

CAS-løsning av ulikheten minus 3 x i andre pluss 27 større enn 0. Utklipp.

1.10.11

Løs ulikhetene.

vis fasit

Vi finner først nullpunktene til uttrykket på venstre side.

Vi vet nå at uttrykket $²$ er lik 0 når og når . Det er bare for disse verdiene av at uttrykket kan skifte fortegn. Vi tar stikkprøver for -verdier i intervallene og .

Vi bruker det faktoriserte uttrykket når vi tar stikkprøvene.

$å å å$

Vi kan da sette opp fortegnslinjen:

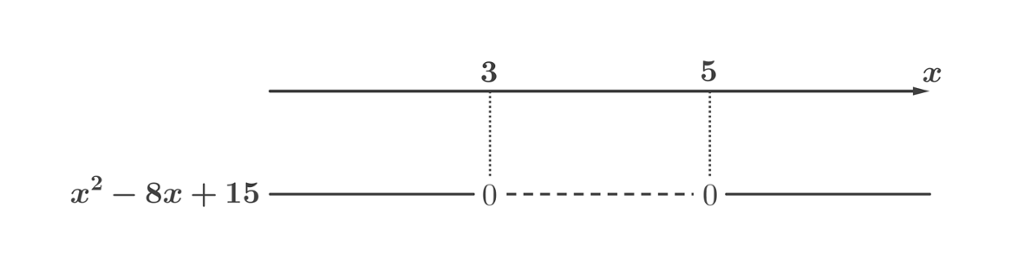
Fortegnslinje for uttrykket x i andre minus 8 x pluss 15 som viser at uttrykket er positivt fra minus uendelig til 3, negativt fra 3 til 5 og positivt fra 5 til pluss uendelig. Utklipp.

Oppgaven vår var å finne ut for hvilke verdier av det stemte at $²$ . Av fortegnslinjen kan vi lese at ulikheten har løsningen .

Løsning med CAS:

CAS-løsning av ulikheten x i andre minus 8 x pluss 15 mindre enn eller lik 0. Utklipp.

vis fasit

Vi ordner først ulikheten slik at vi får 0 på høyre side.

Vi finner så nullpunktene til uttrykket på venstre side.

Vi vet nå at uttrykket $²$ er lik 0 når og når . Det er bare for disse verdiene av at uttrykket kan skifte fortegn. Vi tar stikkprøver for -verdier i intervallene og .

Vi bruker det faktoriserte uttrykket når vi tar stikkprøvene.

$å å å$

Vi kan da sette opp fortegnslinjen:

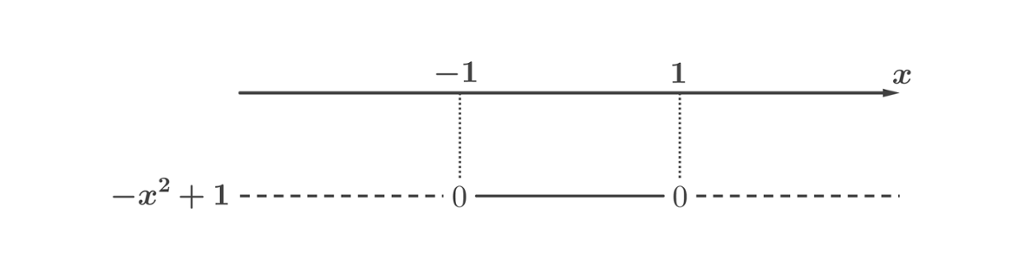
Fortegnslinje for uttrykket minus x i andre pluss 1 som viser at uttrykket er negativt fra minus uendelig til minus 1, positivt fra minus 1 til 1 og negativt fra 1 til pluss uendelig. Utklipp.

Oppgaven vår var å finne ut for hvilke verdier av det stemte at $²$ . Av fortegnslinjen kan vi lese at ulikheten har løsningen .

Løsning med CAS:

CAS-løsning av ulikheten 1 større enn x i andre. Utklipp.

vis fasit

Vi ordner først ulikheten slik at vi får 0 på høyre side.

Vi finner så nullpunktene til uttrykket på venstre side.

Vi vet nå at uttrykket $²$ er lik 0 når og når . Det er bare for disse verdiene av at uttrykket kan skifte fortegn. Vi tar stikkprøver for -verdier i intervallene og .

Vi bruker det faktoriserte uttrykket når vi tar stikkprøvene.

$å å å$

Vi kan da sette opp fortegnslinjen:

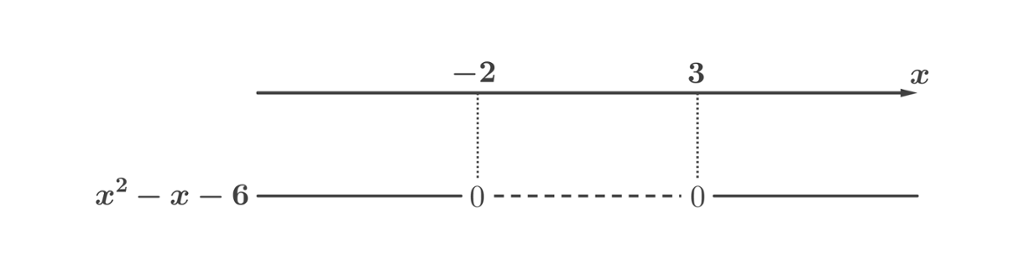
Fortegnslinje for uttrykket x i andre minus x minus 6 som viser at uttrykket er positivt fra minus uendelig til minus 2, negativt fra minus 2 til 3 og positivt fra 3 til pluss uendelig. Utklipp.

Oppgaven vår var å finne ut for hvilke verdier av det stemte at $²$ . Av fortegnslinjen kan vi lese at ulikheten har løsningen .

Løsning med CAS:

CAS-løsning av ulikheten minus x mindre enn eller lik minus x i andre pluss 6. Utklipp.

vis fasit

Vi ordner først ulikheten slik at vi får 0 på høyre side.

Vi finner så nullpunktene til uttrykket på venstre side.

Vi vet nå at uttrykket $²$ er lik 0 når . Det er bare for denne verdien av at uttrykket kan skifte fortegn. Vi tar stikkprøver for -verdier i intervallene og .

Vi bruker det faktoriserte uttrykket når vi tar stikkprøvene.

Det er bare for denne verdien av at uttrykket kan skifte fortegn. Vi tar stikkprøve for -verdi mindre enn 1 og -verdi større enn 1.

$å å$

Vi kan da sette opp fortegnslinjen:

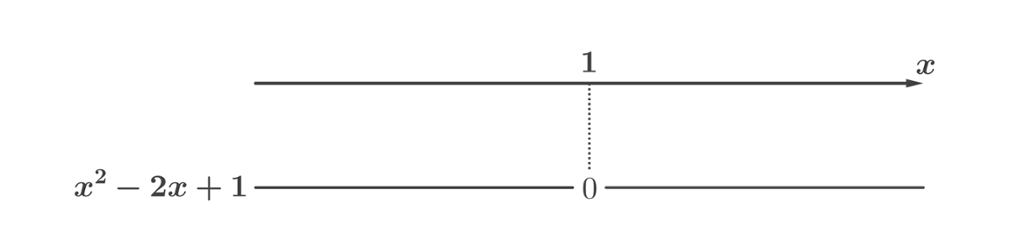
Fortegnslinje for uttrykket x i andre minus 2 x pluss 1 som viser at uttrykket er positivt fra minus uendelig til 1 og positivt fra 1 til pluss uendelig. Utklipp.

Oppgaven vår var å finne ut for hvilke verdier av det stemte at $²$ . Av fortegnslinjen kan vi lese at ulikheten er oppfylt for alle verdier av .

Vi kunne også sett dette direkte da $² ²$ . Dette uttrykket aldri kan bli negativt.

Løsning:

Løsning med CAS:

Merk måten GeoGebra skriver løsningen på her.

vis fasit

Vi ordner først ulikheten slik at vi får 0 på høyre side.

Vi finner så nullpunktene til uttrykket på venstre side.

Likningen har ingen reelle løsninger. Uttrykket kan ikke ha verdien 0. Det betyr at uttrykket enten er negativt hele tiden, eller positivt hele tiden. Hvis vi setter inn , har uttrykket verdien . Med andre ord, uttrykket vil være negativt for alle verdier av .

Ulikheten spør etter når uttrykket er større eller lik 0. Det er det aldri, så ulikheten har ingen løsning.

Løsning med CAS:

CAS-løsning av ulikheten 2 x pluss 3 større enn eller lik x i andre pluss 5. Utklipp.

1.10.12

Forklar hvorfor ulikhetene ikke har noen løsning.

vis fasit

$²$ kan aldri bli negativ. Uttrykket $²$ blir dermed aldri større enn 1.

vis fasit

Verken $²$ eller $²$ kan bli mindre enn 0.

1.10.10

1.10.11

1.10.12

Njuolggadusat teavstta geavaheapmái "Ulikheter av andre grad"