Volum av prisme

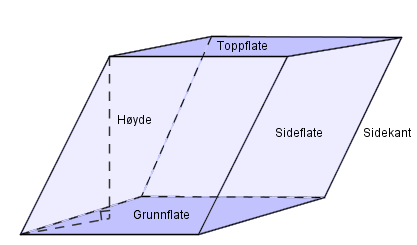
Høyden, $h$ er avstanden mellom grunnflaten, $G$, og toppflaten.

Hvis alle sideflater er rektangler, er prismet rett.

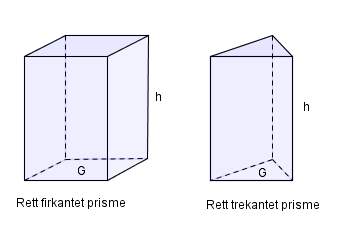
Hvis grunnflaten er en firkant, har vi et firkantet prisme. Hvis grunnflaten er en trekant, har vi et trekantet prisme.

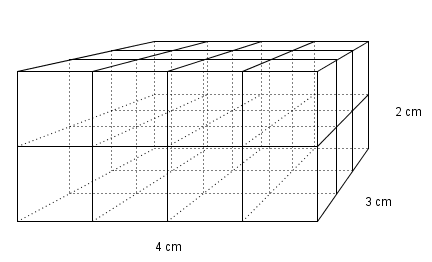
I et rett firkantet prisme med sidekanter i grunnflaten på 4 cm og 3 cm, og med høyde 2 cm kan vi få plass til 24 terninger som hver har et volum på 1 cm³. Det betyr at volumet er på 24 cm³.

Grunnflaten har et areal på

$G=4 \mathrm{cm}·3 \mathrm{cm}=12 {\mathrm{cm}}^2$

Det betyr at vi kan finne volumet til et rett firkantet prisme ved å multiplisere arealet til grunnflaten med høyden.

$V=G·h=12 {\mathrm{cm}}^2·2 \mathrm{cm}=24 {\mathrm{cm}}^3$

Vi får en formel for volumet til et rett firkantet prisme, $V=G·h$

Vi kan, etter samme mønster som ved arealformler, studere forskjellige typer prismer, og overbevise oss om at denne formelen må gjelde for alle prismer.