Konvergens og divergens i uendelege geometriske rekker
1.1.40
Undersøk om dei geometriske rekkene under konvergerer eller divergerer. Dersom dei konvergerer: Finn summen dei konvergerer mot.
a)
Løysing
Vi finn
Sidan vi har at
b)
Løysing
Vi les her ut av formelen at
c)
Løysing
Her les vi ut frå formelen at
d)
Løysing
Vi observerer at dette er den same rekka som i b), altså konvergerer ho, og summen er 6.
e)
Løysing
Vi har her ei geometrisk rekke med
Dette er den same rekka som i a), og summen er dermed
f)
Løysing
Vi skriv om uttrykket for
Vi ser at vi har ei geometrisk rekke med
Vi har at
Vi finn summen:
Her kan vi òg legge merke til at dette er det same som rekka i e) multiplisert med
g)
Løysing
Vi finn
Vi har at
h)
Løysing
Vi skriv om uttrykket for
Vi har dermed at
1.1.41
Finn konvergensområdet til rekkene, og finn eit uttrykk for summen i kvart tilfelle.
a)
Løysing
Vi finn først
Vi må ha at
Summen av rekka blir då
b)
Løysing
Vi finn først
Dette gir det same konvergensområdet som i a), altså
c)
Løysing
Vi må løyse dobbeltulikskapen
Vi deler dobbeltulikskapen i to og løyser dei to enkle ulikskapane kvar for seg.
Venstre ulikskap:
Vi har to kritiske punkt,
Vi har at venstre ulikskap har løysinga
Høgre ulikskap:
Vi har to kritiske punkt,
Vi har at høgre ulikskap har løysinga
Vi må finne det området som oppfyller begge ulikskapane samtidig. Vi teiknar ein figur for å få oversikt:
Dette gir oss konvergensområdet:
Vi finn eit uttrykk for summen:
I GeoGebra kan vi løyse heile denne oppgåva med nokre få tastetrykk:
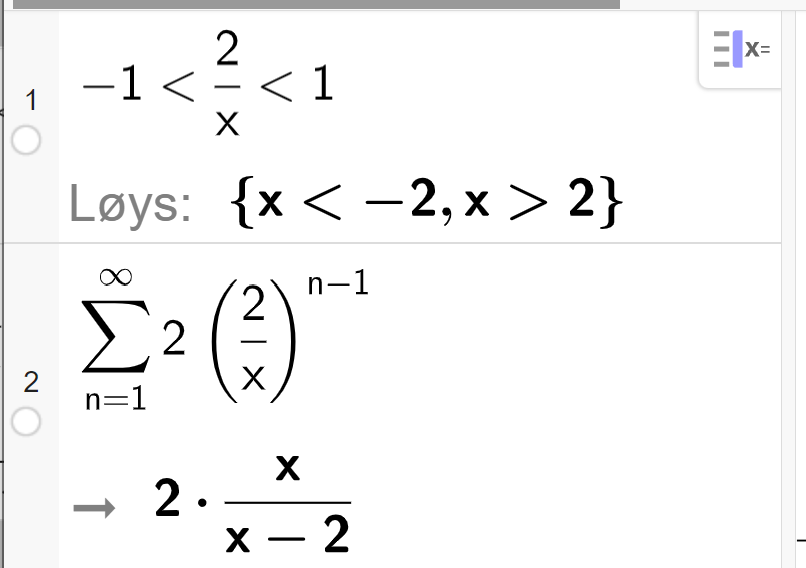
d)
Løysing
Vi startar med å finne
Vi løyser dobbeltulikskapen:
Vi har altså at
Vi les ut av formelen at
e)
Løysing
Vi les ut av formelen at
Vi deler opp i to ulikskapar:
Vi har at konvergensområdet er
For å finne
1.1.42
Ta for deg rekkene i oppgåve 1.1.41, og finn ut om summen av kvar rekke kan bli 1 eller 4. Finn òg ut kva
Løysing a)
For hand:
Vi set formelen vi fann for summen lik 1:
Vi ser at vi får summen lik 1 dersom vi set
Vi gjer det same med 4:
Vi ser at vi får summen lik 4 dersom vi set
Når det gjeld løysing i CAS, kan vi anten bruke formelen for summen vi fann i 1.1.41 slik vi gjorde for hand, eller vi kan bruke den eksplisitte formelen for
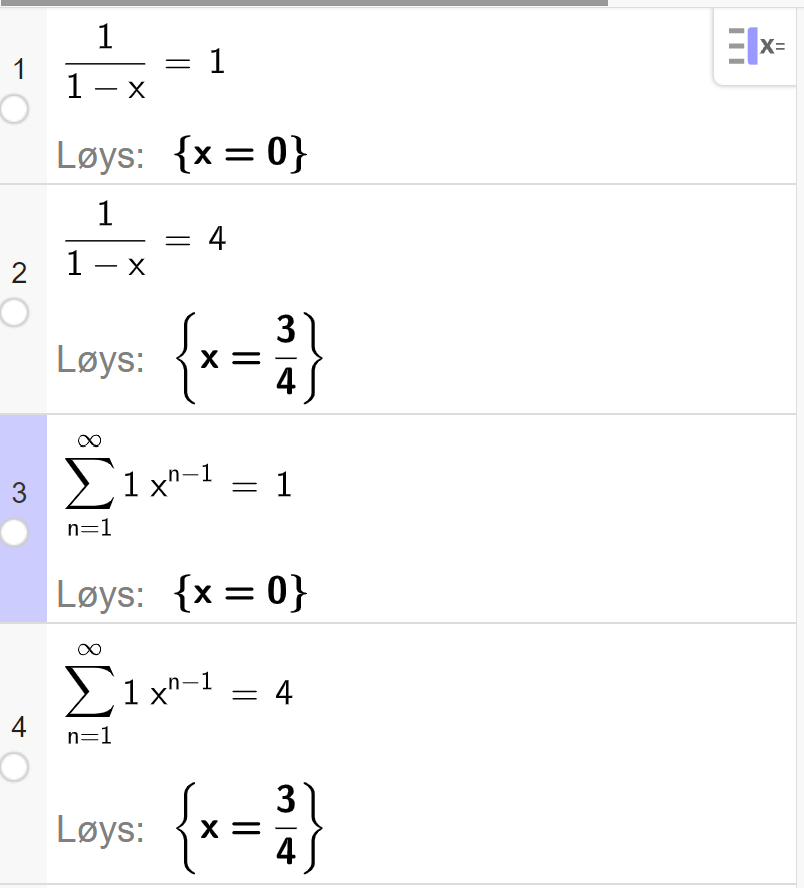
Løysing b)
For hand:
Her ser vi at vi ikkje har noka løysing på likninga, altså kan ikkje summen bli 1.
Her finn vi ei løysing på likninga, men vi ser at ho ligg utanfor konvergensområdet, og derfor kan summen heller ikkje bli 4.
Vi løyser i CAS, her viser vi berre løysinga med summeformel:
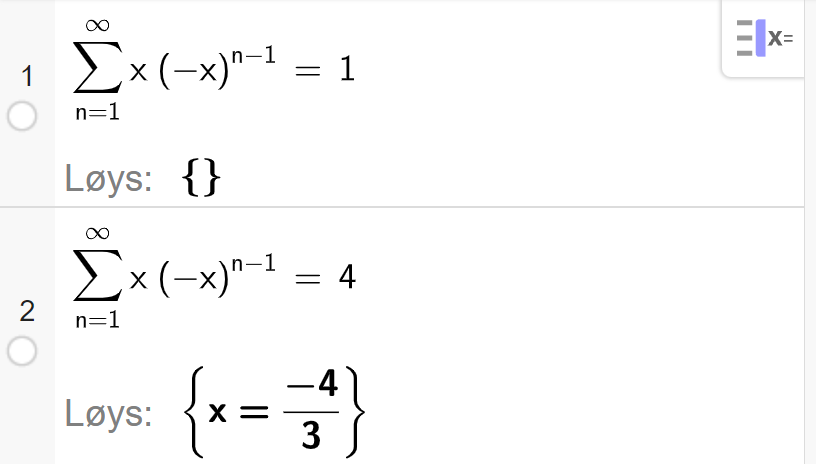
Legg merke til at GeoGebra gir deg eit svar på likninga sjølv om denne summen ikkje finst! Sannsynlegvis finn GeoGebra formelen for summen først, slik vi har gjort, og løyser likninga med han utan å kunne ta med seg konvergensintervallet.
Løysing c)
I resten av desse oppgåvene viser vi berre løysing for hand. Sjå på dei to tidlegare oppgåvene dersom du ikkje hugsar korleis du skal løyse i CAS.
Vi ser at
Denne løysinga er innanfor konvergensintervallet. Det betyr at summen
Løysing d)
Denne løysinga er innanfor konvergensintervallet, så summen blir 1 når
Denne løysinga er òg innanfor konvergensintervallet, så summen blir 4 når
Løysing e)
Vi ser at begge løysingane ligg innanfor konvergensområdet, og vi har at
1.1.43
Ta for deg rekkene i oppgåve 1.1.41 a) og c). Avgjer kva som er den største og den minste summen rekka kan konvergere mot.
Løysing a)
Vi har at summen av rekka er gitt ved
Vi deriverer funksjonen i CAS:
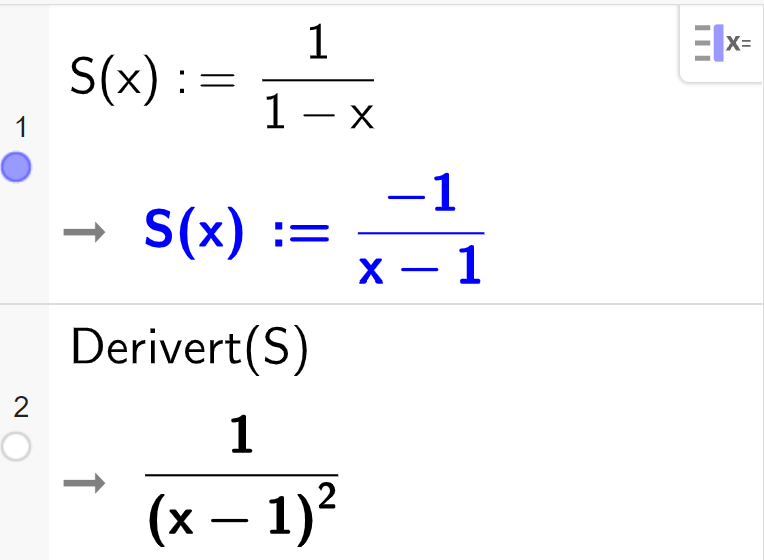
Vi legg merke til at den deriverte alltid er positiv. Det vil seie at funksjonen er strengt veksande i heile konvergensintervallet. Vi kan ikkje finne ein bestemd høgaste verdi og lågaste verdi fordi summen ikkje er definert i ytterpunkta i intervallet, men vi kan finne grenseverdiane til summen.
Den lågaste verdien finn vi ved å la
Den høgaste verdien finn vi ved å la
Vi ser at vi får 0 i nemnaren, men ikkje i teljaren. Det vil seie at uttrykket ikkje har nokon grenseverdi, men vil gå mot uendeleg.
Vi ser at nedre grenseverdi for summen av rekka er
Det kan vere lurt (men ikkje nødvendig!) å kikke på grafen til funksjonen for å få betre oversikt:
Vi ser at det vi fann ved rekning, stemmer bra med biletet av grafen.
Løysing c)
Vi har at summen er gitt ved
Igjen startar vi med å derivere for å undersøke monotonieigenskapane til funksjonen:

Vi legg merke til at den deriverte er negativ i heile konvergensområdet, det vil seie at vi må leite etter den høgaste verdien der
Vi finn desse grenseverdiane:
Vi har altså at den nedre grenseverdien til summen av rekka er 1, og det eksisterer ikkje ein øvre grenseverdi. Vi legg òg merke til at summen ikkje kan bli 2.
Eit tips her òg er å teikne grafen dersom du vil ha betre oversikt.