Rekker

Tenk deg at du får tilbod om å ta ein sommarjobb. Arbeidsgivaren er litt rar og seier at du får 1 krone den første dagen du jobbar. Så doblar han daglønna di for kvar dag du er på jobb. Det vil seie at du får 2 kroner den andre dagen du jobbar, 4 kroner den tredje dagen og så vidare.

Vi kan seie at lønna di ein bestemd dag, dag $$ n$$, er eit ledd i ei geometrisk følge der  $$ a_1=1$$  og  $$ k=2$$. Lønna på dag $$ n$$ er altså

$$ a_n=1·2^{n-1}=2^{n-1}$$

Vi byrjar med å finne samla lønn den første veka, det vil seie dei 5 første arbeidsdagane. Då må vi rekne ut summen av dei fem første ledda i følga:

$$ \begin{array}{rcl}& & a_1+a_2+a_3+a_4+a_5 \\ & =& 2^{\left(1-1\right)}+2^{\left(2-1\right)}+2^{\left(3-1\right)}+2^{\left(4-1\right)}+2^{\left(5-1\right)}\\ & =& 1+2+4+8+16\\ & =& 31\end{array}$$

Lønna den første veka blir på berre 31 kroner!

Men la oss finne ut kor mykje du vil tene på 20 arbeidsdagar med denne ordninga. Vi kunne sjølvsagt ha rekna ut kvart av dei 20 ledda for hand, men det slepp vi. Vi kan bruke ulike digitale hjelpemiddel, her viser vi korleis vi kan finne svaret ved hjelp av Python:

1lonn = 0
2dagar = 20
3
4for n in range(1,dagar + 1):
5    lonn = lonn + 2**(n-1)
6    
7print("Samla lønn blir", lonn, "kr.")

Køyr programmet og finn ut kva den samla lønna blir etter 20 arbeidsdagar.

Over har vi sett eit døme på ei talrekke, eller berre ei rekke. Ei slik rekke får vi når vi adderer ledda i ei følge.

Ledda i ei rekke er dei same som i den tilsvarande følga, og vi bruker dei same symbola for ledda. Det første leddet kallar vi $a_1$, det andre leddet $a_2$ og så vidare.

På same måte som vi skil mellom endelege og uendelege følger, skil vi mellom endelege og uendelege rekker.

Ei endeleg rekke består av eit endeleg tal ledd slik som rekka vi såg på over:

$$ 1 + 2+4+8+10$$

Ei uendeleg rekke består av uendeleg mange ledd slik som

$1+2+3+4+...$

Summen av dei $n$ første ledda i ei rekke blir nemnd med symbolet $S_n$.

$S_n=a_1+a_2+a_3+ ... +a_n$

Vi har ein eigen matematisk skrivemåte for summen av ei rekke. Då bruker vi den greske bokstaven stor sigma: $\mathrm{\Sigma }$. Til dømes skriv vi summen av dei seks første kvadrattala på den følgande måten:

$$ \begin{array}{rcl}{S}_6 & =& \sum _{n=1}^6{n}^2\\ & =& 1^2+2^2+3^2+4^2+5^2+6^2\\ & =& 91\end{array}$$

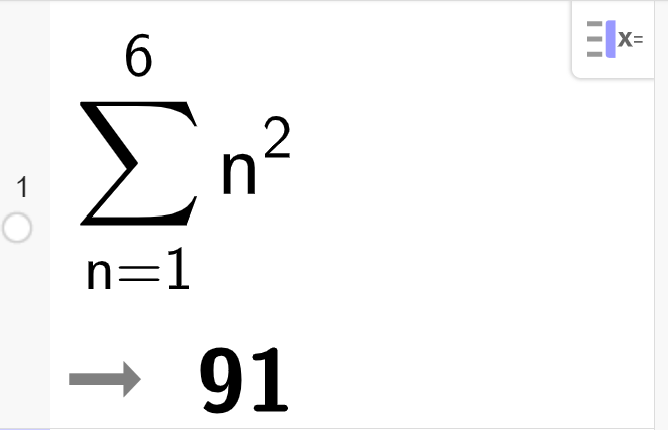
Vi kan rekne ut summen av ei rekke dersom vi kjenner den eksplisitte formelen for $$ a_n$$. Vi bruker kommandoen "Sum(<Uttrykk>,<Variabel>,<Start>,<Slutt>)" . Vi reknar ut summen av dei 6 første kvadrattala i GeoGebra ved å skrive Sum(n2,n,1,6):