Annuitetslån og noverdiar
Før eller sidan får du kanskje behov for å låne pengar. Det kan vere pengar for å kjøpe ein bil eller kanskje ei leilegheit.
Eit lån må betalast tilbake. I tillegg må det betalast renter og gebyr. Dette skjer ved at låntakar betaler eit beløp eit visst tal gonger, eit visst tal terminar.
Dersom det blir betalt eit beløp kvar månad, er det 12 terminar per år. Dersom det berre blir betalt ein gong per år, er det berre ein termin per år. Det er òg vanleg med til dømes fire terminar per år. Då blir det betalt eit beløp kvar tredje månad.
Talet på terminar til saman er lik talet på terminar per år multiplisert med løpetida til lånet i talet på år. Løpetida er kor lenge lånet varer, eller kor lang tid det er frå du tek opp eit lån til det er nedbetalt.
Terminbeløpet, det som blir betalt ein termin, består av ein avdragsdel og ein rentedel og kanskje eit termingebyr. Avdragsdelen, eller avdraget, er den delen av terminbeløpet som går med til å betale ned på lånet. Rentedelen er det vi må betale for å få lov til å ha lånet. I tillegg kan det vere eit termingebyr, eit fast beløp som skal betalast.
Vi skil mellom to typar lån: serielån og annuitetslån. I denne artikkelen skal vi konsentrere oss om annuitetslån.
Den vanlegaste forma for lån er det vi kallar annuitetslån. Dette ordet kjem av det latinske ordet anno, som betyr "i året". Eit slikt lån er kjenneteikna av at du betaler det same beløpet kvar gong gjennom heile perioden du skal betale tilbake lånet, altså at terminbeløpa er like store. Her vil vi operere med lån der du betaler eitt avdrag i året. Dette gjer vi fordi utrekningane elles blir veldig komplekse. Vi vil heller ikkje ta omsyn til eventuelle gebyr.
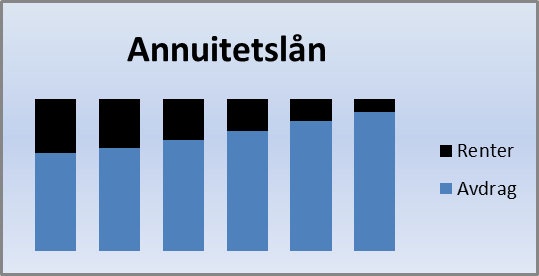
Etter kvart som lånet blir betalt ned, vil renteutgiftene bli mindre. Når terminbeløpet skal vere like stort gjennom heile låneperioden, vil avdragsdelen auke når rentedelen går ned.
Når bankane skal berekne terminbeløpet for eit annuitetslån, bruker dei teorien om geometriske rekker.
Vi skal vise to ulike måtar vi kan rekne oss fram til terminbeløpa på, ut frå lånebeløp, rente og løpetid. I dømet vårt skal vi låne 200 000 kroner til ei årleg rente på 5 prosent. Løpetida skal vere 10 år.
For å forstå korleis bankane reknar ut terminbeløpa, kan vi gjere eit tankeeksperiment. Vi førestiller oss at vi lar lånet stå og vekse i 10 år utan å betale inn noko på det. Kor mykje vil vi skylde banken etter 10 år?
Så tenker vi oss at vi i staden for å betale inn pengar til banken skal spare pengar på ein konto som òg har 5 prosent rente. Det første beløpet set vi inn om eit år, det andre om to år og så vidare. Det første beløpet vi set inn, forrentar seg 9 gonger, mens det siste beløpet vi set inn, ikkje rekk å forrente seg i det heile. Figuren under viser korleis beløpa vi set inn, forrentar seg gjennom dei 10 åra:
Det vi betaler inn til saman, er summen av alle uttrykka som står i kolonnen til høgre:
Kan du finne
Dersom beløpet som står på kontoen etter 10 år, skal vere nok til å betale ned heile lånet, må summen av denne rekka vere lik summen vi skyldar banken. Det gir denne likninga:
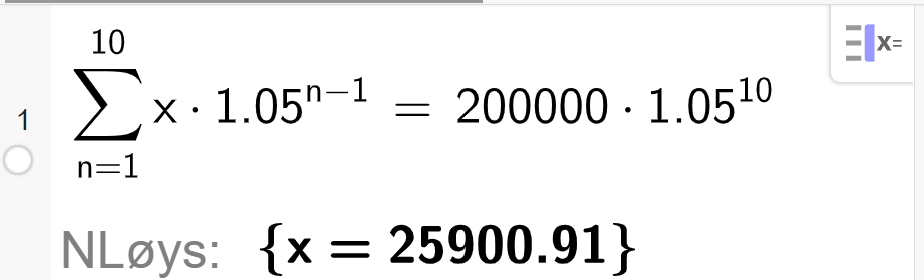
Denne løyser vi enklast i CAS. Vi finn ut at terminbeløpet må vere cirka 25 900 kroner for at lånet skal bli nedbetalt på 10 år.
I dømet over samanlikna vi den framtidige verdien til lånebeløpet og terminbeløpa. Vi kan òg rekne omvendt, det vil seie at vi reknar om dei framtidige innbetalingane til det vil kallar noverdiar. Då må vi hugse på at det beløpet vi betaler inn, inneheld ein del som er rente, og vi må dele på vekstfaktoren ein gong per år akkurat denne delen av lånet har forrenta seg. Studer figuren under nøye. Kva blir
Vi legg saman noverdiane:
Vi ser at det første leddet i rekka,
Ein eksplisitt formel for rekka blir
Summen av noverdiane til terminbeløpa må vere lik det beløpet vi lånte, det gir denne likninga:
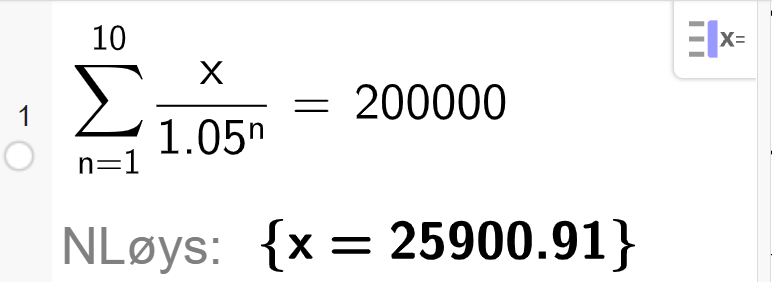
Vi løyser likninga i GeoGebra:
Vi ser at løysinga heldigvis blir akkurat den same som då vi samanlikna framtidige verdiar.