Funksjonar representerte ved grafar og verditabellar. Verdimengd
Vi ser på funksjonen gitt ved
Funksjonen er her representert med ein formel.
Vi kan lage ein verditabell ved først å velje ut nokre verdiar for som ligg i definisjonsområdet. Deretter reknar vi ut dei tilsvarande funksjonsverdiane, . Verditabellen nedanfor viser eit utval av samanhøyrande verdiar for og .
|
|
|
|---|---|---|
Funksjonen er no representert med ein verditabell.
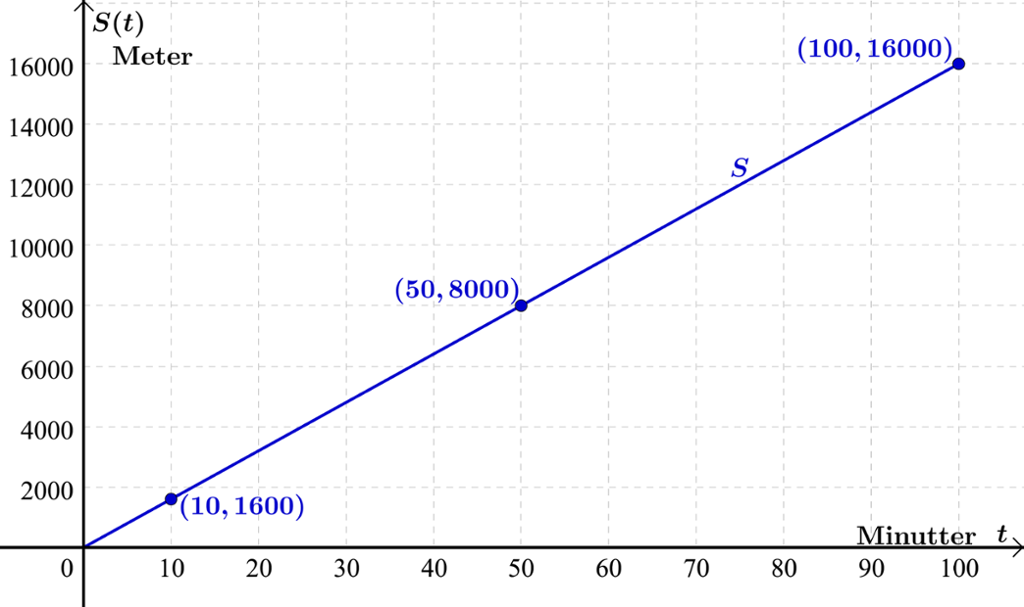
Dei samanhøyrande verdiane frå verditabellen merkjer vi av som punkt i eit koordinatsystem der blir sett av langs førsteaksen og langs andreaksen.
Aksane blir tilpassa slik at alle punkta i verditabellen «får plass» i grafvindauget.
I eksempelet vårt ligg punkta på ei rett linje. Vi trekkjer den rette linja gjennom punkta. Denne linja blir kalla for grafen av funksjonen.
Dersom punkta ikkje ligg på ei rett linje, teiknar vi ei kurve som går gjennom punkta.
Alle punkta som ligg på grafen av funksjonen viser samhøyrande verdi for og .
Funksjonen er no representert med ein graf.
Langs førsteaksen finn vi -verdiane, altså definisjonsmengda til funksjonen. Langs andreaksen finn vi funksjonsverdiane . Vi ser at verdiane langs andreaksen går frå til når -verdiane varierer gjennom definisjonsmengda, . Verdimengda er derfor .