Måleusikkerheit – mål tida mellom to knips
I dette forsøket vert det nytta eit lydprogram som heiter Audacity, men det er fullt mogleg å nytte andre program eller ein mobilapp med dei same funksjonane som Audacity.
Bli bevisst på måleusikkerheit ved å sjå kor vanskeleg det er å måle heilt nøyaktig.
Pass på at det er ganske stille rundt deg. Set i gang eit lydopptak og knips to gonger med eit par sekunds mellomrom. Stopp deretter opptaket og sjå på det. Ser du at dei to knipsa er lette å skilje ut? Ved å bruke musepeikaren kan vi markere området mellom dei, og sjå kor lang tid det tok frå det eine knipset til det andre, ved hjelp av den innebygde tidsmålaren.
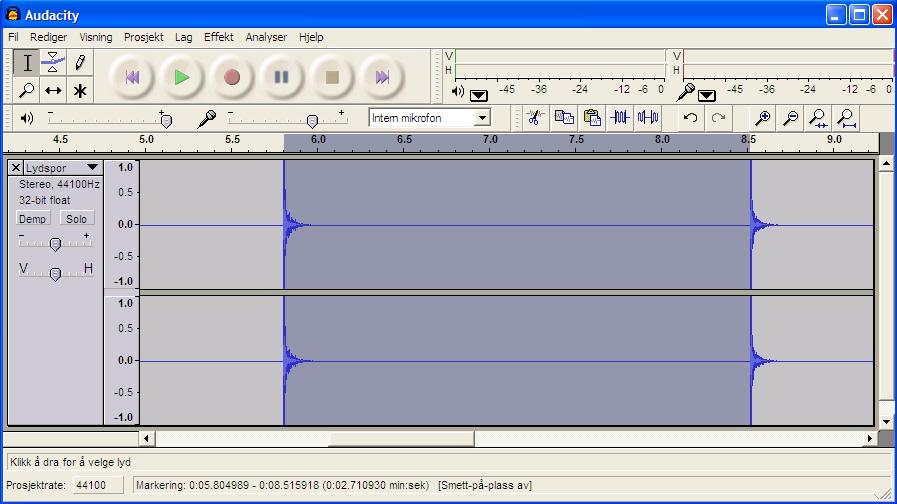
I biletet er perioden mellom dei to knipsa markert, og nedst i biletet ser vi at det har komme inn nokre tidsdata, nemleg kor langt frå starten av opptaket markeringa begynner og sluttar. I tillegg er det rekna ut differansen mellom dei, altså kor langt klippet er. Under ser vi eit forstørra utsnitt av den nedste linja.
Om vi måler fleire gonger, ser vi at vi ofte får ulikt resultat. Fire ulike målingar gav desse resultata:
- 2,710930 sekund
- 2,722540 sekund
- 2,710930 sekund
- 2,716735 sekund
Her legg vi merke til fleire ting:
- Det ser ut som om vi les av resultatet svært nøyaktig, men likevel har vi forskjell allereie i andre siffer bak kommaet. Det er kanskje ikkje så nøyaktig likevel?
- To av målingane er heilt like, er det tilfeldig?
Forskjellen mellom høgaste og lågaste måling er no (2,722540 – 2,710930) sekund = 0,011610 sekund, eller 0,43 % av gjennomsnittet på 2,71528375 sekund for dei fire målingane. For å sjå om det er mogleg å måle meir nøyaktig dersom vi forstørrar biletet, kan vi «dra ut» biletet litt:
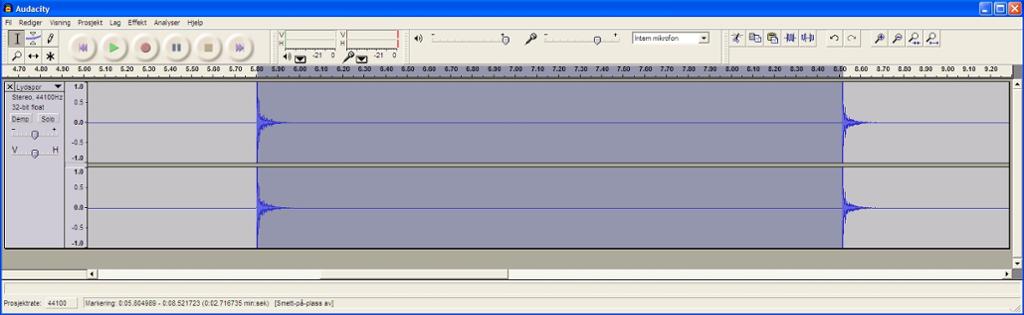
No var det mogleg å finne start og slutt på området litt meir nøyaktig, og det blei avlese:
- 2,713832 sekund
- 2,716735 sekund
- 2,708027 sekund
- 2,710930 sekund
Forskjellen mellom høgaste og lågaste avlesing var no (2,716735-2,708027) sekund = 0,008708 sekund, altså litt mindre enn ved den førre måleserien. Spreiinga av målingane utgjorde no 0,32 % av gjennomsnittet, som var 2,712381 sekund.
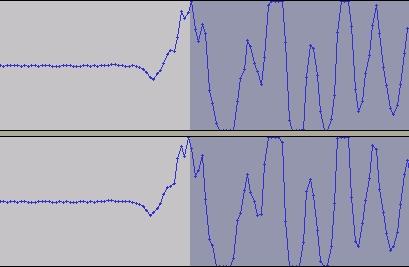
Er det mogleg å måle heilt nøyaktig, tru? Kva om vi forstørrar så mykje at vi ser kvart lydutslag heilt tydeleg? Da ser vi at lydkurvene består av ei mengd punkt som er bundne saman med linjestykke, slik at det blir ei samanhengande lydkurve. Eit punkt beskriv ei lydregistrering, og i dette tilfellet blei det gjort opptak 44100 gonger i sekundet.
I dei to første måleseriane ser vi at vi ikkje er sikre på meir enn første siffer etter komma, og vi må derfor seie at tida mellom dei to knipsa var 2,7 sekund.
I den siste målinga er avstanden mellom dei to første «toppane» i knipset 2,710966 sekund. Det kan vere freistande å seie at det er det heilt rette svaret, men er vi sikre på at det er den første toppen som er starten på knipset? Kanskje er det den svake lyden som kom like før? Og Audacity måler lyden berre 44 100 gonger i sekundet – er det sikkert at programmet fekk med seg det punktet vi er ute etter?
Dersom vi eksperimenterer litt i den store forstørringa, ser vi at vi må nøye oss med å seie at avstanden mellom knipsa var 2,71 sekund.
Lause trådar som det må forskast meir på:
- Tre av målingane var like lange, 2,710930 sekund. Kan det komme av at markøren tilfeldigvis «snappa» seg fast til same punkt fleire gonger?
- Er vi sikre på at tidsmålinga i Audacity er korrekt, eller opererer programmet med ei eiga tidsrekning, litt forskjellig frå resten av verda?
Relatert innhald
Når du skal måle noko, kan du bli usikker på om måleinstrument og metodar er gode nok, men det er mykje du kan gjere for å redusere måleusikkerheita.