Forhold
Forholdet mellom to tal er svaret vi får når vi deler tala på kvarandre.
Dersom vi kallar tala for og , så er forholdet mellom og lik brøken .

Som du ser av definisjonen ovanfor, er forhold i matematikken noko heilt anna enn forholdet til venene dine.
Forholdet mellom tala 5 og 10 er .
Forholdet mellom tala 10 og 5 er .
Vi støyter ofte på forhold i matematikken. Vi skal gi nokre døme på dette, og også sjå på korleis vi kan rekne med forhold.

Vi skal blande saft og vatn. På saftflaska står det oppgitt at blandingsforholdet er . Det vil seie at for kvar del saft, skal vi ha 5 delar vatn.
Til dømes 3 liter rein saft treng vi liter vatn. Det gir 3 liter pluss 15 liter som er 18 liter «saft og vatn».
Til 10 liter vatn treng vi liter rein saft. Det gir 10 liter pluss 2 liter som er 12 liter «saft og vatn».
Men kor mykje rein saft treng vi for å lage 21 liter «saft og vatn»?
Vi må tenkje oss at saftblandinga består av 6 delar, der 1 del er rein saft, og 5 delar er vatn.
Kvar del består av liter. Rein saft utgjer 1 del av blandinga, og då treng vi altså liter rein saft.
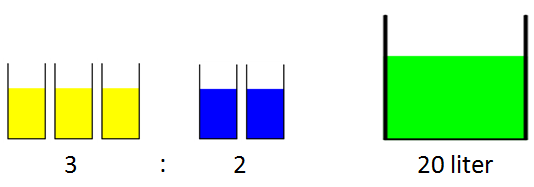

Anders blander gul og blå maling i forholdet for å få grøn maling. Han får til saman 20 liter grøn maling.
Kor mykje gul maling og kor mykje blå maling har han brukt?
3 delar gul maling pluss 2 delar blå maling gir 5 delar. Desse 5 delane svarar til 20 liter.
Kvar del svarar då til
Det er 3 delar gul maling som svarar til .
Det er 2 delar blå maling som svarar til .
Han har brukt 12 liter gul maling og 8 liter blå maling.
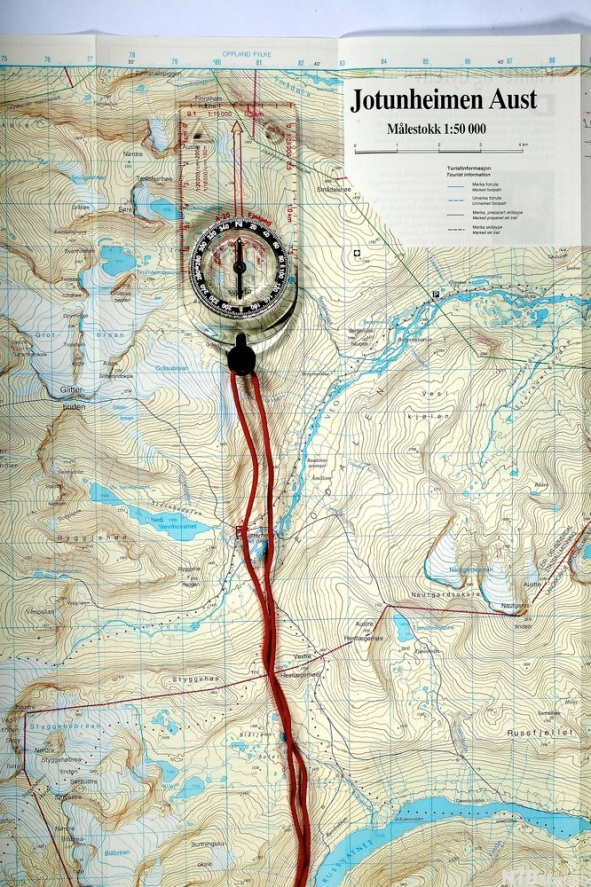
Eit kart har målestokken 1 : 50 000.
Det vil seie at 1 cm på kartet svarar til 50 000 cm i terrenget. Det tyder at forholdet mellom avstandar på kartet og i terrenget er .
Når vi går frå kartet til terrenget, må vi multiplisere med 50 000. Hugs at terrenget er større enn kartet.
cm på kartet svarar til
i terrenget.
Når vi går frå terrenget til kartet, må vi dividere med
50 000. Hugs at kartet er mindre enn terrenget.
km i terrenget svarar til
på kartet.
Valutakursar viser forholdet mellom verdien av ulike valutaer.
Tabellen nedanfor viser verdien av ulike utanlandske valutaer gitt i norske kroner 10.11.2012.
Valuta | 100 DKK | 100 SEK | 1 EUR | 1 GBP | 1 USD |
|---|---|---|---|---|---|
Verdi i NOK | 97,4 | 84,9 | 7,279 | 9,125 | 5,72 |

Vi ser at 1 USD (amerikansk dollar) kostar norske kroner, NOK.
Då vil 20 USD koste .
100 DKK (danske kroner) kostar 97,4 NOK.
Det vil seie at 1 DKK kostar .
20 DKK vil då koste .
Vi går altså «vegen om 1».
Når vi skal gå motsatt vei, må vi dividere på «prisen for 1».
For 80 NOK får vi .
For 80 NOK får vi .
Dette er heilt tilsvarande rekningsmåte som ved kjøp av til dømes eple. Dersom prisen for eitt kg eple er 14 kroner, så må vi for 4 kg eple betale . Tilsvarande får vi for 49 kroner

Vi ser ein person avbilda ved sida av ein mur som vi frå før av kjenner høgda av. Kan vi då rekne ut høgda til personen ut frå bildet?
Vi veit at muren i røyndomen er m høg. Vi måler så høgda til muren på bildet og finn at den er 7 cm.
Då kan vi rekne ut forholdet mellom verkelege høgder og høgder på bildet til
Vi måler så høgda til personen på bildet til 3 cm.
Høgda av personen er i røynda lik