Regresjon

Regresjonsanalyse eller regresjon betyr for oss at vi har nokre samhøyrande verdiar for to variablar og prøver å finne ein samanheng mellom dei, ein samanheng i form av ein funksjon. Dette er det motsette av progresjon, som vi vanlegvis gjer der vi har modellen (funksjonen), og reknar ut samhøyrande verdiar for dei to variablane.

I dømet nedanfor kastar Camilla ein ball opp i lufta. Vi måler høgda $$ h$$ ballen har $$ x$$ sekund etter at han har forlate handa, og ønsker å finne ein matematisk funksjon $$ h\left(x\right)$$ som passar best mogleg til måleresultata. Til det bruker vi eit digitalt verktøy.

Camilla kastar ein ball rett opp i lufta. Tabellen viser høgda til ballen $h$ i meter etter $x$ sekund.

Her har vi samhøyrande verdiar for dei to variablane tid $$ x$$ og høgde $$ h$$. Vi ønsker å komme fram til ein matematisk modell, ein funksjon, for høgda som passar med tala i tabellen. Funksjonen, $$ h\left(x\right)$$, må vere slik at dersom vi set til dømes $$ x=1,5$$, bør funksjonen gi eit svar nær 11,9. Vi kan bruke eit digitalt verktøy som GeoGebra eller programmering til denne jobben.

Regresjon med GeoGebra

Vi skriv tala inn i reknearkdelen i GeoGebra, markerer tala og vel verktøyet "Regresjonsanalyse" frå den andre verktøymenyen øvst oppe. Sjå figuren nedanfor.

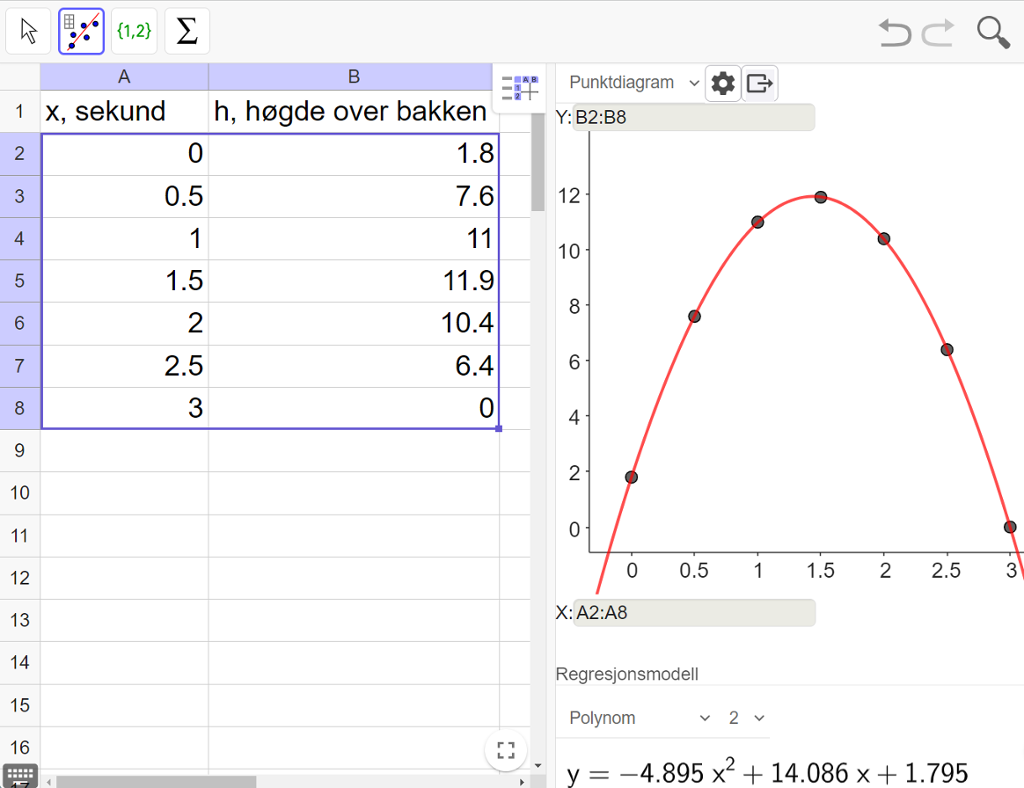
Først kjem berre punkta frå reknearket opp. Grafen får vi først når vi vel ein regresjonsmodell. Sidan punkta ser ut som dei kan ligge på ein parabel, vel vi "Polynom" og "2" for å få ein andregradsfunksjon. GeoGebra bereknar då at den andregradsfunksjonen som passar best med tala, er

$$ h\left(x\right)=-4,8952x^2+14,0857x+1,7952$$

Vi kan sjå at grafen til denne funksjonen passar svært godt til målepunkta. Det skjer ikkje alltid.

For å få grafen over i det vanlege grafikkfeltet trykker vi på knappen med ein firkant og ei pil på øvst i regresjonsanalyseverktøyet og vel "Kopier til grafikkfeltet". Då kan vi lage ei skikkeleg grafisk framstilling av resultata og setje namn på aksane.

Regresjon med Python

Regresjon med Python kan gjerast på fleire måtar. Her har vi valt å bruke metoden curve_fit frå scipy.optimize sjølv om han gir oss meir data enn vi skal bruke her.

Metoden er basert på at vi skriv i koden kva slags type funksjon som skal brukast i den matematiske modellen. Dette gjer vi ved å definere modellen som ein eigendefinert pythonfunksjon, som vi vel å kalle modell. I vårt tilfelle ønsker vi å tilpasse målingane til ein andregradsfunksjon av typen $$ h\left(x\right)=a{x}^2+bx+c$$. Den eigendefinerte pythonfunksjonen modell kan då sjå slik ut:

1def modell(x,a,b,c):
2  return a*x**2 + b*x + c

Parametrane til modell er først den frie variabelen x, deretter konstantane som skal brukast i modellfunksjonen, som vi naturleg nok kallar a, b og c. Funksjonen modell blir brukt av metoden curve_fit saman med ei liste med $$ x$$-verdiane og ei liste med $$ y$$-verdiane i målingane. curve_fit gir tilbake to lister. Den eine inneheld dei tre konstantane a, b og c som gjer at den matematiske funksjonen vi definerte i modell, passar mest mogleg med måledataa. Den andre lista inneheld dei såkalla kovariansane, som vi ikkje skal bruke her.

Koden for heile programmet kan sjå slik ut:

1        # importerer nødvendige bibliotek
2from scipy.optimize import curve_fit
3import numpy as np
4import matplotlib.pyplot as plt
5
6        # lagar funksjonen som beskriv modellen
7def modell(x,a,b,c):
8  return a*x**2 + b*x + c
9  
10        # legg inn måledataa i lister
11x_verdiar = [0,0.5,1,1.5,2,2.5,3]
12y_verdiar = [1.8,7.6,11,11.9,10.4,6.4,0]
13
14        # bruker metoden curve_fit og legg resultata i to lister
15konstantar,kovarians = curve_fit(modell,x_verdiar,y_verdiar)
16
17        # hentar ut konstantane frå lista konstantar
18a, b, c = konstantar
19
20        # lagar utskrift av funksjonen
21print(f"Funksjonen blir h(x) = {a:.2f}x^2 {b:+.2f}x {c:+.2f}.")
22
23        # plottar data
24plt.plot(x_verdiar,y_verdiar,'o', label = "Målingar")
25
26        # plottar modell
27x_array = np.linspace(min(x_verdiar),max(x_verdiar),300)
28y_array = modell(x_array,a,b,c)
29plt.plot(x_array,y_array,"brown", label = "Modell")
30plt.legend(bbox_to_anchor=(1,1))
31plt.xlabel("$x$, tid i sekund") # tittel på x-aksen
32plt.ylabel("$h$, høgde i meter ")
33plt.grid(True)
34plt.show()

Køyring av koden gir denne utskrifta:

"Funksjonen blir h(x) = -4.90x^2 +14.09x +1.80."

Vi får same funksjon $$ h$$ som med regresjon med GeoGebra. Det er ikkje alltid tilfelle sidan ulike program kan bruke ulike måtar å komme fram til funksjonane på.