Fagstoff

Krummingsforhold og vendepunkt. Dobbeltderiverttesten

Vi kan ha god nytte av den andrederiverte, eller den dobbeltderiverte, til ein funksjon.

Funksjonen $f$ er gitt ved

$f (x) = \frac{1}{3} x^{3} - \frac{1}{2} x^{2} - 2 x + 1$

Denne funksjonen er òg drøfta i døme 2 på sida Analyse av polynomfunksjonar ved rekning.

Vi deriverer funksjonen to gonger. Då får vi den andrederiverte eller den dobbeltderiverte $f^{''} (x)$ . Legg merke til skrivemåten, no med to apostrofar.

$\begin{array}{l} f (x) = \frac{1}{3} x^{3} - \frac{1}{2} x^{2} - 2 x + 1 \\ f^{'} (x) = x^{2} - x - 2 \\ f^{''} (x) = 2 x - 1 \end{array}$

Vi teiknar forteiknslinja til $f'' (x)$ og grafen til sjølve funksjonen i det same koordinatsystemet.

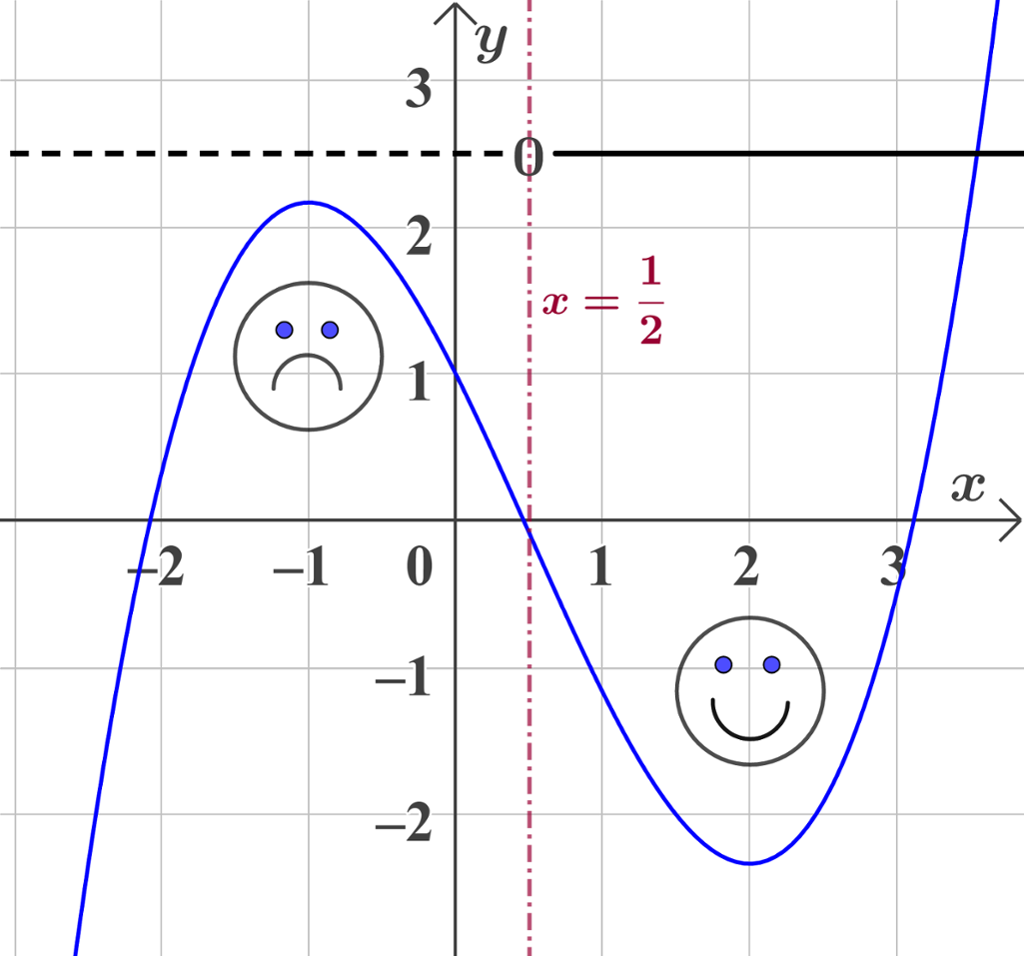
Grafen til f av x er lik 1 tredels x i tredje minus 1 halv x i andre minus 2 x pluss 1 er teikna i eit koordinatsystem for x-verdiar mellom minus 2,5 og 3,5. Forteiknslinja for f dobbeltderivert av x er også teikna. Linja er stipla når x er mindre enn ein halv, null når x er lik 1 halv og heiltrekt når x er større enn ein halv. Eit surt fjes er teikna i det området der grafen til f vender den hole sida si ned, og eit smilefjes er teikna i det området der grafen til f vender den hole sida si opp. Linja x er lik 1 halv er teikna inn. Skjermutklipp.

Det viser seg at

ein graf vender den hole sida si opp når $f^{''} (x) > 0$ . Han krummar oppover.
ein graf vender den hole sida si ned når $f^{''} (x) < 0$ . Han krummar nedover.
ein graf kan ha eit vendepunkt når $f^{''} (x) = 0$

At grafen vender den hole sida si opp, $f^{''} (x) > 0$ , betyr at den deriverte veks. Det vil seie at sjølve funksjonen anten veks meir og meir eller minkar mindre og mindre.

At grafen vender den hole sida si ned, $f^{''} (x) < 0$ , betyr at den deriverte minkar. Det vil seie at sjølve funksjonen minkar meir og meir eller veks mindre og mindre.

Vendepunkt

Eit punkt på grafen der grafen skifter mellom å vende den hole sida si ned og å vende den hole sida si opp, eller motsett, kallar vi eit vendepunkt. Vi kan òg seie at grafen endrar krumming.

Den deriverte (dersom han eksisterer!) har anten den største verdien sin eller den minste verdien sin i vendepunktet. Det vil seie at funksjonen veks raskest eller minkar raskast i vendepunktet.

Har vi alltid eit vendepunkt dersom den dobbelderiverte er lik 0?

Svar

Nei, det har vi ikkje.

Teikn grafen til $f (x) = x^{4}$ i GeoGebra. Du vil sjå at grafen "er blid" overalt.

Men dersom vi dobbeltderiverer, får vi

$\begin{array}{rcl} f (x) & = & x^{4} \\ f^{'} (x) & = & 4 x^{3} \\ f^{''} (x) & = & 12 x^{2} \end{array}$

Det vil seie at den dobbeltderiverte har eit nullpunkt for $x = 0$ utan at funksjonen har eit vendepunkt.

Det vi må sjå på her, er om den dobbelderiverte skifter forteikn i nullpunktet, sidan eit vendepunkt er definert som eit punkt på grafen der grafen endrar krumming. $12 x^{2} \geq 0$ for alle $x \in ℝ$ , så derfor har vi ikkje eit vendepunkt i dette tilfellet.

Kan vi ha eit vendepunkt utan at den dobbeltderiverte er lik 0?

Svar

Ja, det kan vi ha.

Teikn grafen til $g (x) = \sqrt[5]{x^{3}}$ i GeoGebra. Ser du at grafen har den hole sida opp for $x < 0$ og den hole sida ned for $x > 0$ ?

Dersom vi deriverer to gonger, vil vi sjå at verken den deriverte eller den dobbeltderiverte er definert i punktet $x = 0$ .

Men sjølve funksjonen er definert og har eit vendepunkt for $x = 0$ .

Vi hugsar at vi har eit vendepunkt dersom funksjonen endrar krumming i dette punktet, altså dersom den dobbeltderiverte har ulikt forteikn på kvar side av punktet. Det kan skje i eit punkt der den dobbeltderiverte er null, eller i eit punkt der den dobbeltderiverte ikkje er definert, slik som i dette tilfellet.

Under har vi teikna grafen til $g (x)$ saman med grafen til den dobbeltderiverte:

På biletet er g av x lik femterota av x i tredje teikna inn som grøn graf. Den dobbeltderiverte av x er teikna inn som blå graf. Skjermutklipp.

Definisjon av vendepunkt

Vi ønskjer oss ein formell definisjon på kva som er eit vendepunkt. Vi har til no vist at vi må ha eit punkt på grafen der den dobbeltderiverte skiftar forteikn. Legg merke til at det ikkje er eit krav at den deriverte eller den dobbeltderiverte må eksistere i dette punktet, men det er eit krav at sjølve funksjonen må vere definert her. I tillegg til dette er det eit krav om at funksjonen må vere kontinuerleg i dette punktet. Nokre matematikarar krev i tillegg at det skal vere mogleg å teikne ein tangent i eit punkt for at det skal kunne definerast som eit vendepunkt, men vi vel her definisjonen som berre krev kontinuitet.

Då kan vi få den følgjande definisjonen:

Eit punkt $(a, f (a))$ på grafen til ein funksjon $f (x)$ er eit vendepunkt dersom $f (x)$ er kontinuerleg for $x = a$ og $f^{''} (x)$ har motsett forteikn for $x < a og x > a$ i eit område rundt $a$ .

Vendetangent

I oppgåver blir vi ofte bedde om å finne likninga for ein vendetangent. Ein vendetangent er tangenten til funksjonen i eit vendepunkt.

Døme

Vi vil finne likninga for vendetangenten til funksjonen $f$ gitt ved

$f (x) = \frac{1}{3} x^{3} - \frac{1}{2} x^{2} - 2 x + 1$

Dette er den same funksjonen som vi brukte i dømet øvst på sida. Vi deriverer først funksjonen to gonger.

$\begin{array}{rcl} f (x) & = & \frac{1}{3} x^{3} - \frac{1}{2} x^{2} - 2 x + 1 \\ f^{'} (x) & = & x^{2} - x - 2 \\ f^{''} (x) & = & 2 x - 1 \end{array}$

Vi set så den dobbeltderiverte lik null.

$\begin{array}{rcl} f^{''} (x) & = & 0 \\ 2 x - 1 & = & 0 \\ x & = & \frac{1}{2} \end{array}$

Vi har òg at $f^{''} (0) = - 1$ og $f^{''} (1) = 2 \cdot 1 - 1 = 1$ . Det viser at vi har eit vendepunkt for $x = \frac{1}{2}$ .

$f (\frac{1}{2}) = \frac{1}{3} {(\frac{1}{2})}^{3} - \frac{1}{2} {(\frac{1}{2})}^{2} - 2 (\frac{1}{2}) + 1 = - \frac{1}{12}$

Det betyr at koordinatane til vendepunktet er $(\frac{1}{2}, - \frac{1}{12})$ .

Vi reknar så ut stigingstalet til tangenten i vendepunktet:

$f^{'} (\frac{1}{2}) = {(\frac{1}{2})}^{2} - \frac{1}{2} - 2 = - \frac{9}{4}$

No veit vi at vendetangenten går gjennom punktet $(\frac{1}{2}, - \frac{1}{12})$ og har stigingstalet $- \frac{9}{4}$ . Vi kan då bruke eittpunktsformelen og finne likninga for tangenten.

$\begin{array}{rcl} y - y_{1} & = & a (x - x_{1}) \\ y - (- \frac{1}{12}) & = & - \frac{9}{4} (x - \frac{1}{2}) \\ y + \frac{1}{12} & = & - \frac{9}{4} x + \frac{9}{8} \\ y & = & - \frac{9}{4} x + \frac{9}{8} - \frac{1}{12} \\ y & = & - \frac{9}{4} x + \frac{25}{24} \end{array}$

Vi har til slutt teke med ei oversikt over forteiknslinja til sjølve funksjonsuttrykket saman med forteiknslinjene til den første- og andrederiverte. Desse er teikna inn i koordinatsystemet saman med $f (x)$ .

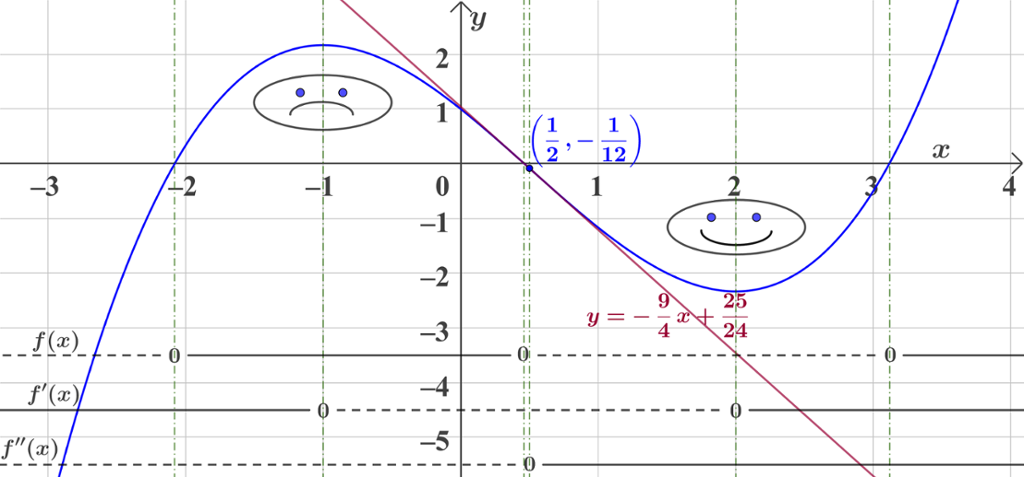
Grafen til f av x er lik 1 tredels x i tredje minus 1 halv x i andre minus 2 x pluss 1 er teikna i eit koordinatsystem for x-verdiar mellom minus 3 og 3,5. Forteiknslinja for f dobbeltderivert av x er også teikna. Linja er stipla når x er mindre enn ein halv, null når x er lik 1 halv og heiltrekt når x er større enn ein halv. Forteiknslinja for f derivert av x er teikna. Linja er heiltrekt når x er mindre enn minus 1, null når x er lik minus 1, stipla når x er større enn minus 1 og mindre enn 2, null når x er lik 2 og heiltrekt når x er større enn 2. Forteiknslinja til f av x er også teikna. Ho er stipla når x er mindre enn minus 2,1, null når x er lik 2,1, heiltrekt når x er større enn minus 2,1 og mindre enn 0,45, null når x er lik 0,45, stipla når x er større enn 0,45 og mindre enn 3,15, null når x er lik 3,15 og heiltrekt når x er større enn 3,15. Eit surt fjes er teikna i det området der grafen til f vendar den hole sida si ned, og eit smilefjes er teikna i det området grafen til f vendar den hole sida si opp. Skjermutklipp.

På grunnlag av forteiknslinjene er det mogleg å teikne ei skisse av grafen. Motsett kan vi ut frå grafen teikne dei tre forteiknslinjene. Ved hjelp av grafen kan vi altså tolke grunnleggjande eigenskapar ved funksjonen.

Toppunkt eller botnpunkt? Dobbeltderiverttesten

CAS-utrekning med GeoGebra. På linje 1 er det skrive f av x kolon er lik 1 tredels x i tredje minus 1 halv x i andre minus 2 x pluss 1. Svaret er det same. På linje 2 er det skrive f derivert av x er lik 0. Svaret med N Løys er x er lik minus 1 eller x er lik 2. På linje 3 er det skrive f dobbeltderivert av minus 1. Svaret er minus 3. På linje 4 er det skrive f dobbeltderivert av 2. Svaret er 3. På linje 5 er det skrive f av minus 1. Svaret er 13 seksdelar. På linje 6 er det skrive f av 2. Svaret er minus 7 tredelar. Skjermutklipp.

Vi har brukt forteiknslinje til den deriverte for å avgjere om eit ekstremalpunkt er eit toppunkt eller eit botnpunkt.

Den dobbeltderiverte gir oss ein ny metode for å avgjere dette.

Gitt funksjonen $f (x)$ definert i CAS-vindauget.

Sidan $f^{'} (- 1) = 0$ og $f^{''} (- 1)$ er negativ, har grafen hol side ned og eit toppunkt for $x = - 1$ .

Sidan $f^{'} (2) = 0$ og $f^{''} (2)$ er positiv, har grafen hol side opp og eit botnpunkt for $x = 2$ .

Grafen har toppunkt $(- 1, \frac{13}{6}) .$

Grafen har botnpunkt $(2, - \frac{7}{3}) .$

CC BY-SASkrive av Olav Kristensen, Stein Aanensen og Tove Annette Holter.

Sist fagleg oppdatert 16.08.2023