Modell for folketalsutviklinga i Noreg
I år 2000 var det nokre skuleelevar som laga ein modell for folketalsutviklinga i Noreg.
Dei tok utgangspunkt i ein tabell frå Statistisk sentralbyrå (SSB). Tabellen viste folketalet i Noreg for nokre utvalde år i perioden frå 1950 til 2000 (sjå under).
Årstal | 1950 | 1960 | 1970 | 1980 | 1990 | 2000 |
|---|---|---|---|---|---|---|
Folketal | 3 249 954 | 3 567 707 | 3 863 221 | 4 078 900 | 4 233 116 | 4 478 497 |
Det er ein samanheng mellom årstal etter 1950 og folketalet.
Elevane laga ein ny tabell der er talet på år etter 1950 og der er folketalet i millionar.
0 | 10 | 20 | 30 | 40 | 50 | |
|---|---|---|---|---|---|---|
3,2 | 3,6 | 3,9 | 4,1 | 4,2 | 4,5 |
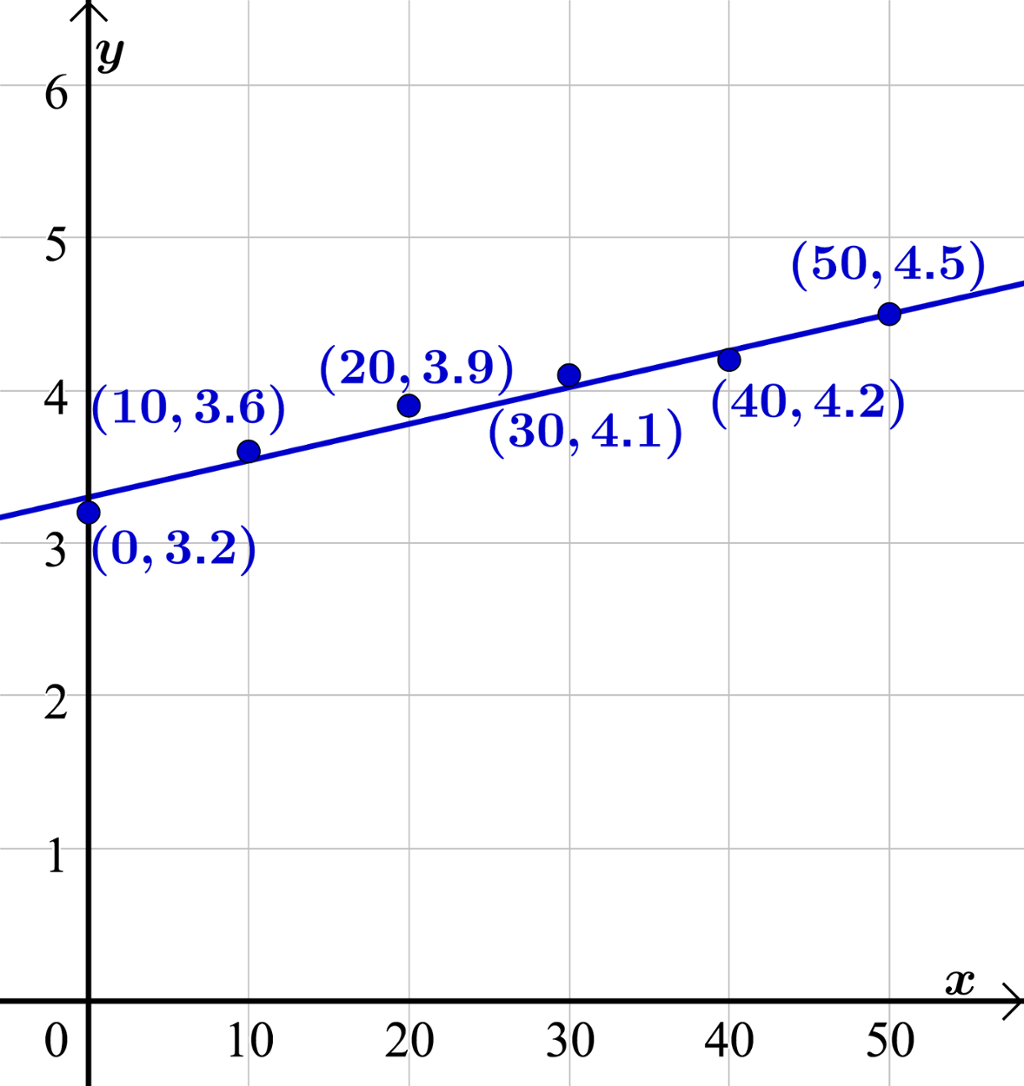
Dei plotta punkta frå den siste tabellen i eit koordinatsystem og såg at punkta låg på ei tilnærma rett linje.
Det betyr at folketalet i Noreg har hatt ein tilnærma lineær vekst i perioden frå 1950 til 2000.
Ved lineær regresjon i GeoGebra kan vi finne ein lineær modell.
Vel «Rekneark». Legg punkta frå tabellen inn i kolonne A og B i reknearket.
Merk området A1:B6.
Vel så «Regresjonsanalyse» og «Analyser».
Vel regresjonsmodell «Lineær».
Vi har då funne at er ein matematisk modell som tilnærma skildrar utviklinga i folketalet i Noreg frå 1950 til 2000.
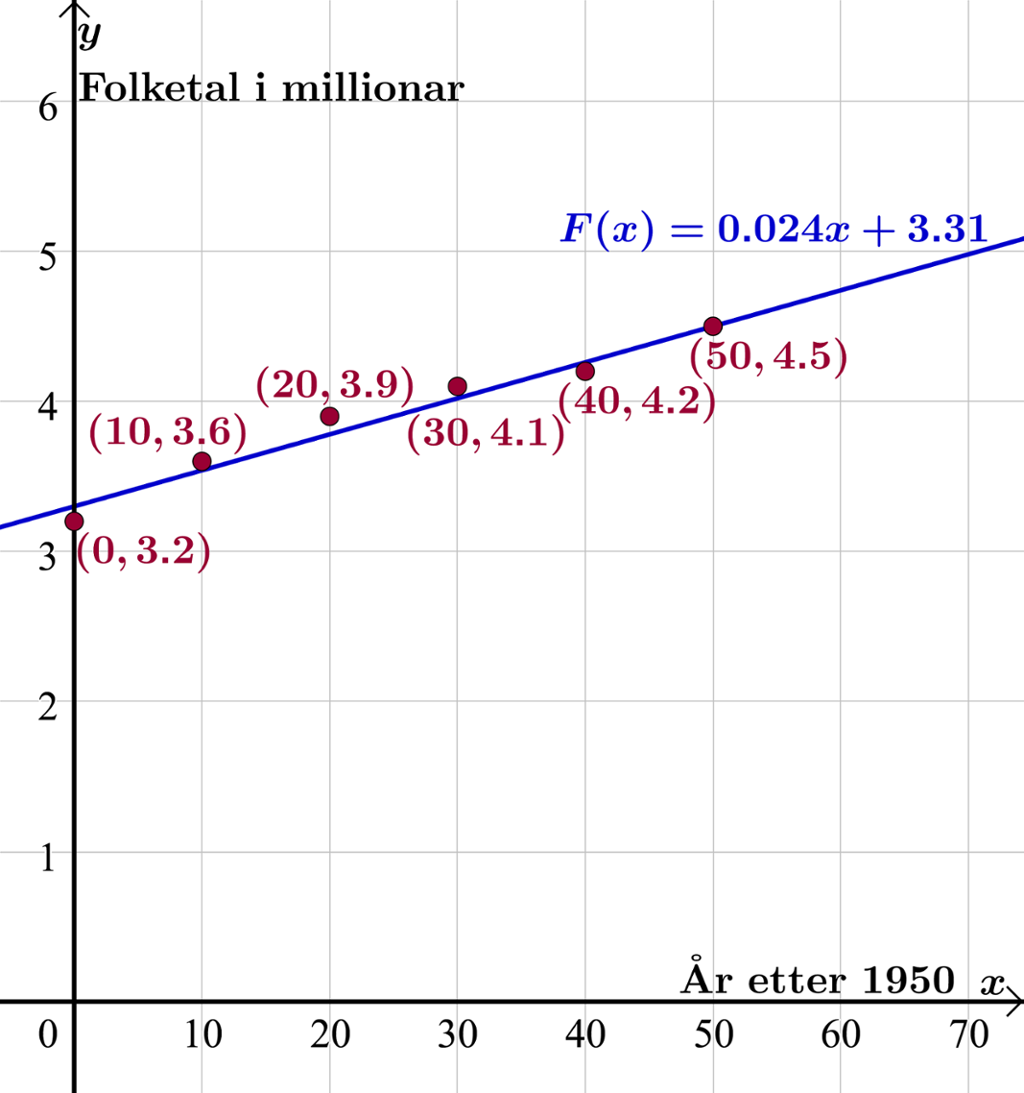
Vel «Kopier til grafikkfeltet».
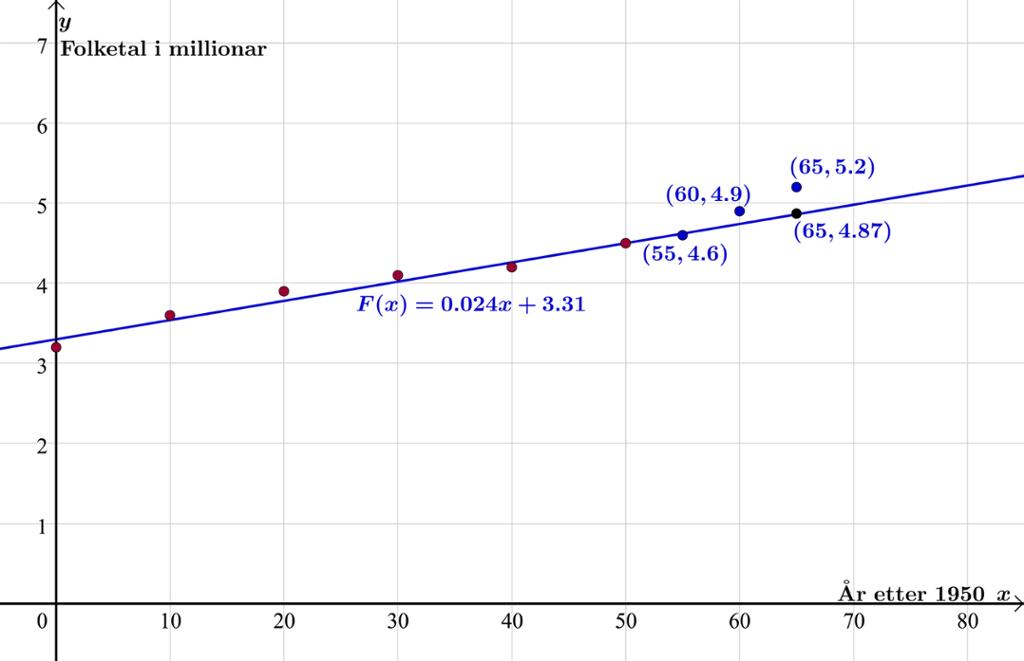
Vi ser at modellen passar godt med punkta.
Stigningstalet er . Det betyr at etter denne modellen aukar folketalet i Noreg i gjennomsnitt med 24 000 personar per år, og folketalet vil vere 4,87 millionar i år 2015. Sjå det svarte punktet på grafen nedanfor.
Tal frå SSB syner at folketalet i Noreg var 4,6 millionar i 2005 og 4,9 millionar i 2010. Det passerte 5,2 millionar i 2015. Sjå dei blå punkta i diagrammet. Folketilvekst i 2014 var ifølgje SSB på 56 749 personar.
Synest du modellen frå år 2000 var ein god modell til å føresjå folketalsutviklinga i åra 2000 til 2015?
Undersøk kva folketalet i Noreg er i dag.
Meiner du at modellen frå år 2000 framleis kan brukast til å føresjå framtidig folketalsutvikling, eller bør det lagast nye modellar?