Praktiske eksempel med eksponentialfunksjonar

Dersom du set kroner i banken i dag og får rente på pengane, kan du om eitt år ta ut kroner
Etter to år kan du ta ut kroner
Etter tre år kan du ta ut kroner
Etter år kan du ta ut kroner .
Talet kallar vi for vekstfaktoren.
Inneståande beløp, , er ein funksjon av talet på år i banken, , og funksjonsuttrykket blir
Funksjonen blir kalla ein eksponentialfunksjon sidan den variable opptrer som eksponent i ein potens.
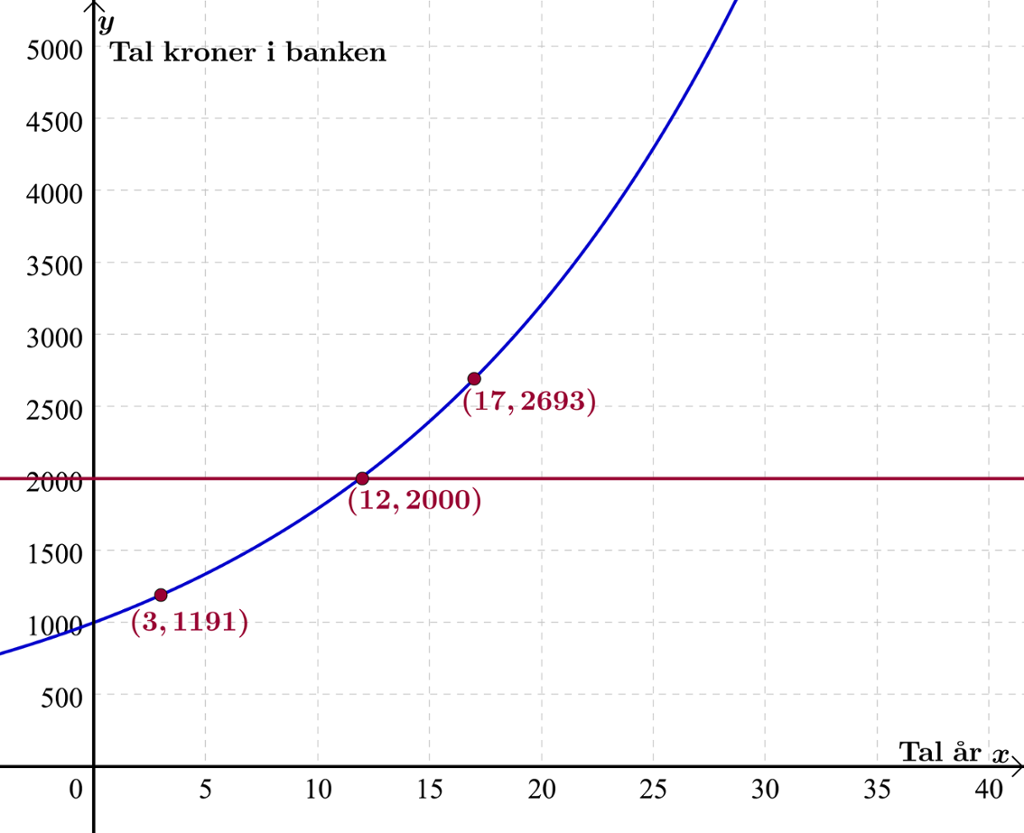
Grafen av funksjonen viser til dømes at beløpet på kroner har vakse til kroner etter år (som vi rekna ut ovanfor) og til kroner etter år.
Kor lenge må pengane stå i banken før beløpet er dobla?
Vi finn svaret ved å teikne den rette linja i same koordinatsystem som grafen av og så finne skjeringspunktet mellom linja og grafen. Pengane må stå i banken i år.
Dette kan vi òg finne ved rekning.
Vi set talet på år pengane må stå i banken lik og får likninga
Dette er ei eksponentiallikning.
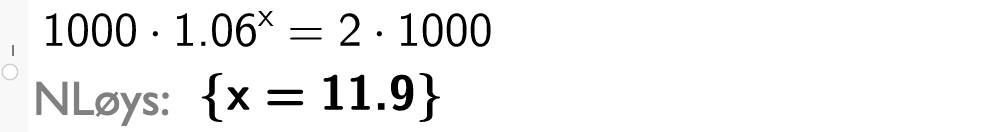
Denne likninga løyser vi ved CAS i GeoGebra

Kari kjøper ein fire år gammal bil for kroner. Bilen har sokke i verdi med kvart år sidan han var ny. Kari reknar med at verdien vil søkke på same måte dei neste åra.
Når har verdien til bilen sokke til halvparten av det Kari betalte for han, og kva kan vi rekna med at verdien var då han var ny?
Verdien på bilen eitt år etter at Kari kjøpte han blir kroner
Verdien på bilen år etter at Kari kjøpte han blir kroner
Verdien av bilen, , år etter at Kari kjøpte han, er då gitt ved
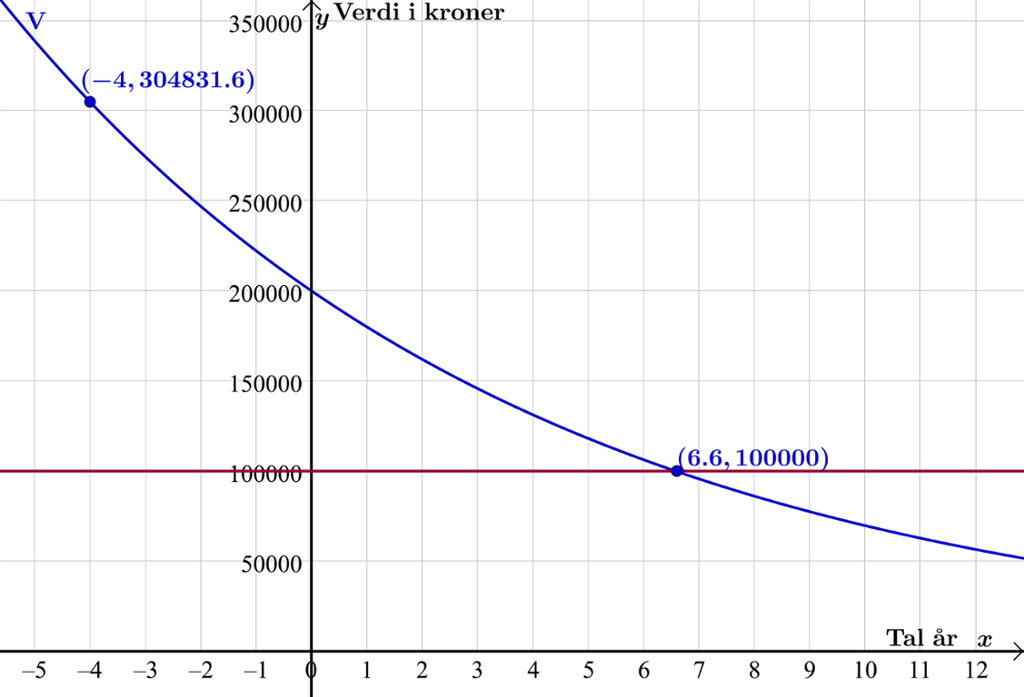
Vi teiknar grafen av .
Vi teiknar den rette linja og finn skjeringspunktet mellom denne og grafen av . Då ser vi at bilen er verdt 100 000 kroner om cirka seks og eit halvt år. Så skriv vi i inntastingsfeltet og får eit nytt punkt på grafen til . Då ser vi at bilen kosta om lag 305 000 kroner då han var ny.
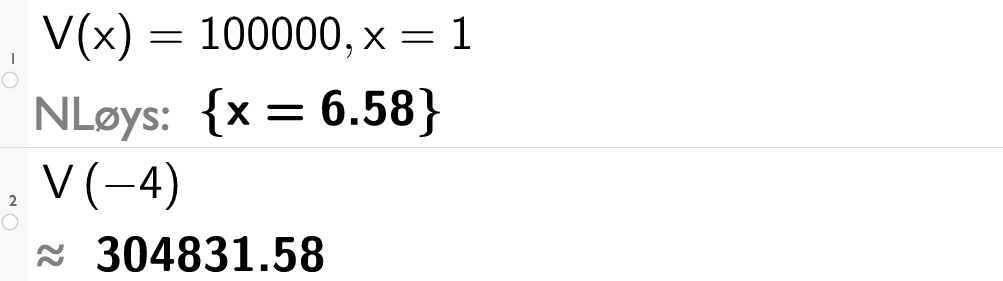
Vi kan finne det same ved rekning. Hugs at du ikkje treng definere funksjonen på ny når han finst i algebrafeltet.