Vinkelsummen i ein n-kant
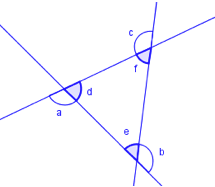
Tenk deg at du spaserer éin runde langs linjestykka på yttersida av ein trekant. Når du går frå eitt linjestykke til eit anna, endrar du retning slik som vinklane a, b og c på figuren viser. Til saman endrar du retning 360°. Det vil seie at
Summen av vinklane i trekanten er .
Vinkelsummen i ein trekant er 180 gradar.
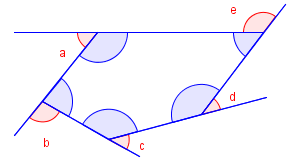
No gjer vi det same med ein femkant. Tenk deg at du spaserer éin runde langs linjestykka på yttersida av ein femkant. Når du går frå eitt linjestykke til eit anna, endrar du retning slik som vinklane a, b, c, d og e på figuren viser. Til saman endrar du retning 360°. Det vil seie at
Då kan vi rekne ut summen av vinklane i femkanten
Vinkelsummen i ein femkant er 540 gradar.
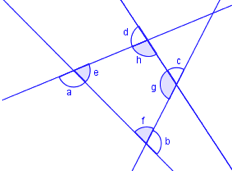
Prøv sjølv, bruk figuren, før tilsvarande bevis som for vinkelsummen i ein trekant og ein femkant, og overbevis deg sjølv om at setninga nedanfor må vere riktig.
Vinkelsummen i ein firkant er 360 gradar.
Vi fekk også eit anna resultat av utrekningane.
- Vinkelsummen i ein 3-kant er
- Vinkelsummen i ein 4-kant er
- Vinkelsummen i ein 5-kant er
Vi kan gjere tilsvarande resonnement for alle mangekantar.
Vinkelsummen i ein n-kant
Vinkelsummen i ein n-kant er .