Sektordiagram
La oss tenkje oss at Mary Ann har gjennomført ei undersøking og funne at følgjande karakterar vart gitte på ei matematikkprøve:
4 2 5 3 3 2 5 4 1 3 2 2 5 3 1 4 2 5 3 2 4 3 6 2 5 3 2 5 5 4
Eit sektordiagram passar spesielt godt til å vise kor stor del ein verdi eller kategori i eit talmateriale utgjer i forhold til heilskapen.
Vi ser igjen på karakterfordelinga på matematikkprøva i klassen til Mary Ann.
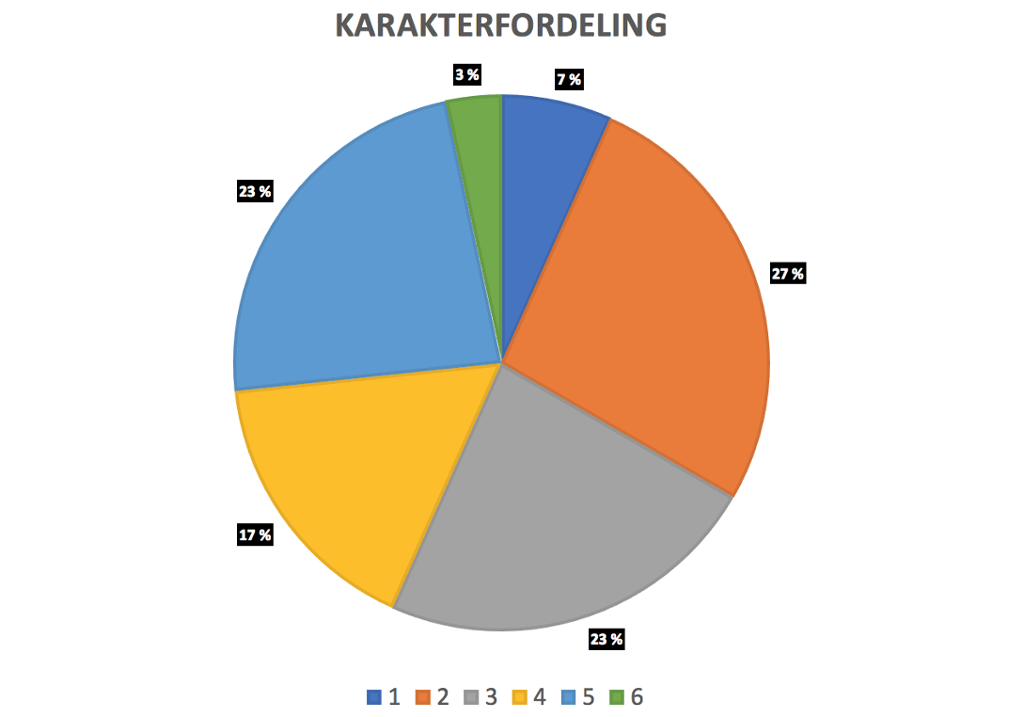
I reknearket Excel merkar vi frekvenskolonnen og vel «Set inn» og ønskt sektordiagram. Ved å velje «Utforming» kan vi finne fram til ønskt oppsett og format for diagrammet.
Arealet av kvar sirkelsektor illustrerer delen elevar som har fått den aktuelle karakteren.
For å teikne eit sektordiagram på papir treng vi ein passar og ei gradskive. Før vi kan teikne, må vi gjere nokre utrekningar.
Vi kan dele ein sirkel inn i 360.
Sidan det til saman er 30 elevar i klassen, må kvar elev tilsvare av sirkelen.
Vi kan då setje opp følgjande tabell:
Karakter | Frekvens | Grader |
|---|---|---|
1 | 2 | 2 · 12° = 24° |
2 | 8 | 8 · 12° = 96° |
3 | 7 | 7 · 12° = 84° |
4 | 5 | 5 · 12° = 60° |
5 | 7 | 7 · 12° = 84° |
6 | 1 | 1 · 12° = 12° |
No kan vi teikne ein sirkel ved hjelp av ein passar og bruke gradskiva til å merke av storleiken på sirkelsektorane.
Legg merke til at 1 % alltid svarar til .