Forenkling av rasjonale uttrykk
Hugsar du at vi kallar eit tal som kan skrivast som ein brøk med heile tal i teljaren og nemnaren, for eit rasjonalt tall?
På same måte er eit typisk rasjonalt uttrykk ein brøk med bokstavuttrykk i teljaren og i nemnaren.
Du kan bruke dei reknereglane du no har lært, til å forenkle og trekke saman rasjonale uttrykk. Reknereglane for brøkrekning gjeld sjølvsagt òg om du erstattar tal med bokstavar.
Vi ønsker å skrive eit rasjonalt uttrykk så enkelt som mogleg. For å få til dette vil vi faktorisere teljaren og nemnaren, for så å undersøke om vi kan forkorte bort nokre faktorar. Vi viser korleis vi går fram ved hjelp av eit døme:
Vi skal forkorte uttrykket .
🤔 Tenk over: Vi ser at vi har fleire ledd både i teljaren og i nemnaren. Kvifor seier vi likevel at dette er eit einledda uttrykk?
Vi startar med å faktorisere teljaren og nemnaren kvar for seg:
Vi kan no skrive om det opphavlege uttrykket. Vi forkortar dei faktorane som er både i teljaren og i nemnaren og får
Ofte må vi trekke saman uttrykk før vi kan forkorte dei. Dette gjeld dersom vi har fleire ledd. Vi viser dette med eit døme òg.
Vi skal trekke saman uttrykket
Det første vi må gjere, er å få sett uttrykket på ein felles brøkstrek. Då må vi finne den minste fellesnemnaren. Det gjer vi ved å faktorisere begge nemnarane. Nemnaren i det andre leddet her er allereie lineær og kan ikkje faktoriserast meir, mens nemnaren i det første leddet kan faktoriserast ved hjelp av konjugatsetninga:
Vi legg merke til at nemnaren i andre ledd er lik ein av faktorane i nemnaren i første ledd. Fellesnemnaren til dei to brøkane blir derfor
Til slutt faktoriserer vi teljaren og forkortar faktor mot faktor der dette er mogleg:
Trinnvis framgangsmåte
Vi faktoriserer nemnarane for å finne fellesnemnaren.
Vi utvider brøkane slik at alle brøkane har lik nemnar.
Vi set ledda på ein felles brøkstrek og reknar ut teljaren.
Vi faktoriserer teljaren.
Vi forkortar faktorane som er like i teljaren og nemnaren.
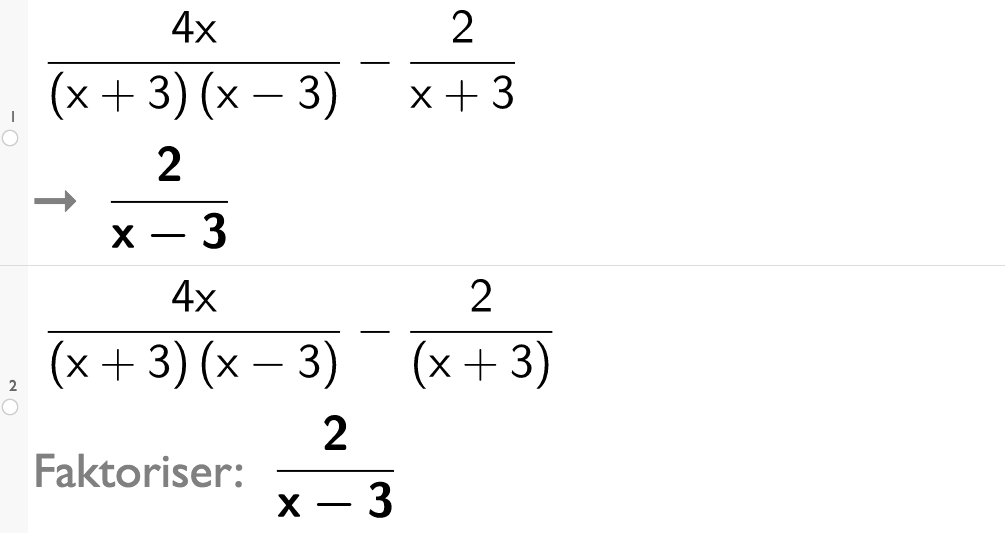
I GeoGebra skriv vi inn uttrykket og trykker enter eller vel verktøyknappen for faktorisering, den fjerde knappen frå venstre.
Du kan òg bruke kommandoen "Faktoriser(uttrykket)".