Meir om forenkling av rasjonale uttrykk
Gjennom tre eksempel skal vi illustrere korleis vi ved hjelp av reglane for brøkrekning og faktoriseringsreglane kan trekkje saman og forenkle rasjonale uttrykk som òg inneheld andregradsuttrykk. Lengst nede på sida finn du korleis vi løyser oppgåvene med CAS i GeoGebra.
Hugsar du at eit tal som kan skrivast som ein brøk med heile tal i teljar og nemnar, blir kalla eit rasjonalt tal? På same måte er eit typisk rasjonalt uttrykk ein brøk med bokstavuttrykk i teljar og nemnar.
Vi skal forkorte brøken
Først faktoriserer vi teljaren ved stiremetoden. Då må vi finne to tal som har produkt lik 6 og sum lik . Tala oppfyller desse krava. Det betyr at
.
Då er
Vi skal forkorte brøken
Først faktoriserer vi teljaren ved stiremetoden. Då må vi finne to tal med produkt lik 2 og sum lik 3. Tala 1 og 2 oppfyller desse krava. Det betyr at
Då er
Vi skal trekkje saman og forkorte
Først faktoriserer vi nemnarane. Vi startar med å finne nullpunkta til nemnaren .
Nemnaren i den tredje brøken har altså nullpunkta .
Det gir at .
Nemnaren i den første brøken faktoriserer vi slik:
Det betyr at fellesnemnaren for dei tre nemnarane er
Då er
Brøkar som blir utvida og forkorta endrar ikkje verdi.
- Når ein brøk blir utvida, blir teljar og nemnar multiplisert med det same talet. Brøken endrar ikkje verdi.
- Når ein brøk blir forkorta, blir teljar og nemnar dividert med det same talet. Brøken endrar ikkje verdi.
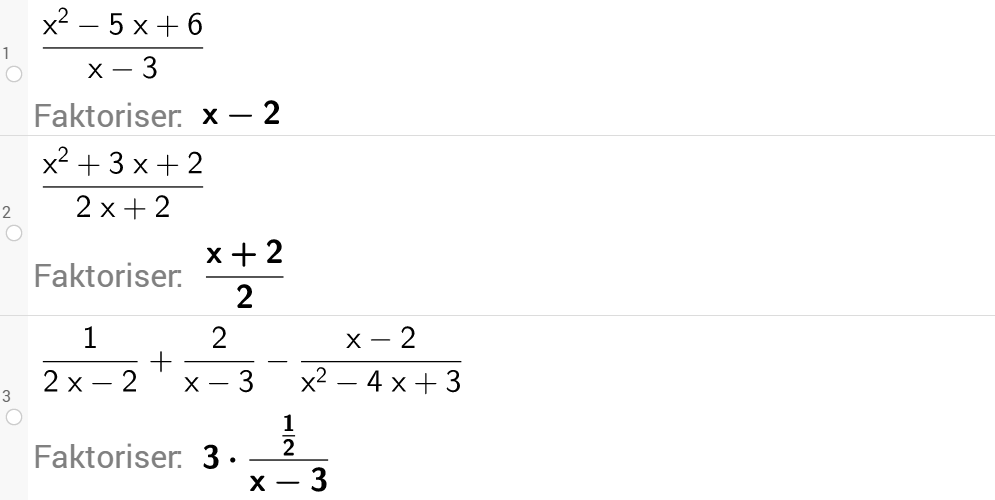
Ved CAS i GeoGebra får vi dei same løysingane som i eksempla over ved å bruke faktoriseringskommandoen.