PID regulatorparametrar

Ein parameter er eit tal i ein matematisk formel som eigentleg er konstant, men som likevel går an å endre på. Dei tre parametrane i PID-regulatoren er vanlegvis konstante, men vi kan endre på dei om vi ikkje er fornøgde med korleis regulatoren fungerer.

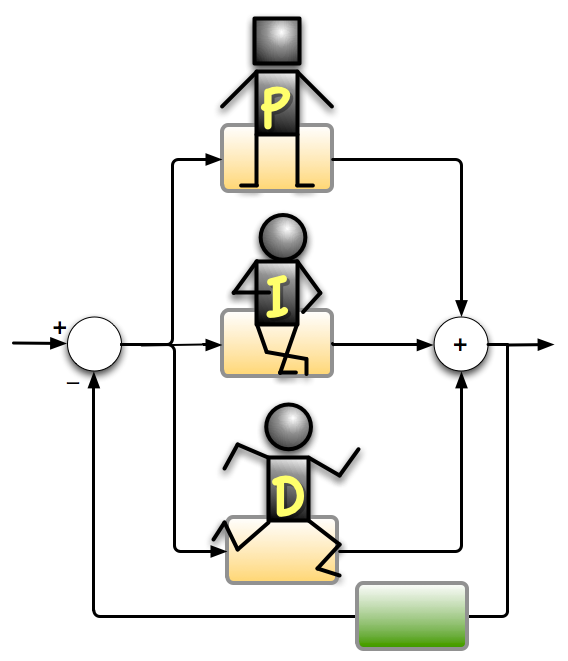
Viss vi tenker oss at vi bruker ein PID-regulator som cruisekontroll på ein bil, vil P-operatøren styre innsprøytningssystemet med eit pådrag som er proporsjonalt med avviket. Tenk deg at cruisekontrollen er stilt til 60 km/t, og at den verkelege farten din er 50 km/t. Avviket er då 10. Dette svarer til ei viss mengde luft og drivstoff i innsprøytningssystemet. Så aukar farten til 55 km/t. Då blir avviket halvert til 5. Dermed blir òg pådraget halvparten av kva det var tidlegare.

I-operatøren tar tida til hjelp, og i ein cruisekontroll samanliknar han tida det tar å køyre ein viss distanse (til dømes 100 meter), med tida det ville ha tatt dersom bilen hadde køyrt i den farten som er stilt inn (skal-verdien). Om dei ikkje er like, prøver han å korrigere for dette.

Til slutt har vi D-operatøren. Han følgjer med på akselerasjonen. Når bilen går i jamn fart, er akselerasjonen lik 0. Viss han ikkje er 0, betyr det at farten aukar eller minkar. Dette prøver D-operatøren å kompensere for.

Dersom det tar veldig lang tid å komme seg til skal-verdien, eller viss reguleringssløyfa heile tida svingar over og under skal-verdien, må vi justere regulatoren (vi seier at vi “tuner” regulatoren). Dei tre parametrane vi kan justere på, er:

• $K_p$ – dette er forsterkinga av P-leddet i regulatoren, eller for å seie det på ein annan måte: Dette er talet P-operatøren gongar med når han gjer jobben sin.
• $T_i$ – denne parameteren blir kalla integraltid. Viss du set denne til eit stort tal, slår du av I-operatøren slik at han ikkje får noko å seie lenger (10 000 er eit stort og fint tal). Viss du derimot set Ti til eit lite tal, vil PID-regulatoren raskt komme til skal-verdien. Brukar du eit tal som er for lite, vil regulatorsløyfa svinge mykje.
• $T_d$ – denne parameteren blir kalla derivattid. Dersom du set denne til 0 (null), slår du av D-operatøren slik at han ikkje får noko å seie lenger. Når $T_d$ har ein passeleg verdi, vil reguleringssløyfa komme meir presist inn på skal-verdien (og ikkje gå så mykje over eller under). Men om verdien for $T_d$ er for høg, kan reguleringssløyfa bli veldig ustabil! Det er ikkje alltid nødvendig å bruke D-operatøren, og ofte lagar han mykje urolegheiter. Han blir derfor ofte slått av.

Eigentleg kunne ein godt tenke seg at ein berre brukte P-operatøren for å regulere. Då hadde jo regulatoren vorte mykje enklare fordi ein berre hadde hatt eitt ledd å halde seg til.

P-operatøren jobbar altså på den måten at han gongar avviket med ein konstant og sender resultatet vidare til pådragsorganet:

$\mathrm{P}={\mathrm{K}}_{\mathrm{p}}·\mathrm{avvik}$

Ser du nøye på formelen, oppdagar du kanskje eit problem. P-operatøren vil berre endre pådraget dersom avviket endrar seg. Om avviket er det same heile tida, vil pådraget òg vere det same heile tida. Og så lenge pådraget er det same, vil ikkje avviket bli mindre!