Rasjonale tal, reelle tal og talintervall
Du kjenner også til rekneoperasjonen divisjon. Vi kan dividere 8 med 4 og få 2, som er eit heilt tal. Men dersom vi til dømes dividerer 1 med 2, blir resultatet ikkje eit heilt tal. Vi får brøken . For å kunne dividere heile tal, må vi på nytt utvide talmengda vår. Vi må inkludere alle tal som består av brøkar med heile tal i teljar og nemnar.
Hugs at i ein brøk er teljaren "på toppen" og nemnaren "nede".
Tal som kan skrivast som brøkar med heile tal i teljar og nemnar, kallar vi rasjonale tal. Desse symboliserer vi med .
Rasjonale tal blir ofte enklare å handsame dersom vi skriv dei som desimaltal. Prinsippet er at vi gjer brøkane om til brøkar med 10, 100, 1000, osv. som nemnarar.
Tenk deg at du deler ei kake i ti like store delar. Fem av desse delane utgjer då halvparten av kaka.
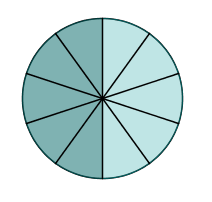
Det tyder at .
Eit desimaltal har eit desimalskiljeteikn. I Noreg bruker vi komma som desimalskiljeteikn, medan dei fleste andre land, og dei fleste digitale verktøy bruker punktum. Første siffer etter desimalskiljeteiknet seier kor mange tidelar vi har, det neste kor mange hundredelar vi har osv. Sifra framfor desimalskiljeteiknet heiltal.
Det tyder at brøken kan skrivast som .
Alle brøkar kan på tilsvarande måte gjerast om til desimaltal.
Til dømes er
Vi kan no nytte rekneoperasjonane addisjon, subtraksjon, multiplikasjon og divisjon på rasjonale tal og få eit rasjonalt tal som resultat.
Har vi så fått med oss alle tala? Svaret er nei.
Bruk til dømes GeoGebra. Lag sirklar i ulik storleik og finn forholdet mellom omkrins og diameter. Forklar kvifor vi kan finne omkrinsen av ein sirkel ved hjelp av formelen når vi kjenner radius.

Forholdet mellom omkrinsen og diameteren i ein sirkel er lik det talet som vi kallar (pi). Du har lært at er ein god tilnærma verdi for , men faktisk er det ikkje mogleg å skrive som eit rasjonalt tal. I 2009 vart talet rekna ut med ein presisjon på 2 699 999 990 000 desimalar. Det vil seie nesten billionar desimalar. Talet er eit reelt tal, men er altså ikkje rasjonalt. Vi seier at det er irrasjonalt.
Eit anna irrasjonalt tal er det talet som multiplisert med seg sjølv gir talet 2. Vi skriv berre . Det finst ingen brøkar som multiplisert med seg sjølv gir talet 2.
Vi må altså utvide talmengda vår igjen for å få med slike tal som og . Den talmengda vi no har fått, kallar vi for dei reelle tala, og vi symboliserer ho med bokstaven .
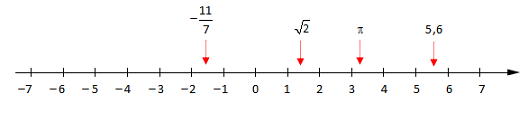
Vi kan tenkje oss alle reelle tal som punkt på ei uendeleg lang rett linje, tallinja. Punkta ligg svært tett. Mellom to reelle tal er det uendeleg mange reelle tal. Spørsmålet er så om vi no har fått med oss alle tal? Svaret er igjen nei.
Det finst til dømes ikkje noko reelt tal som multiplisert med seg sjølv gir talet . er eit imaginært tal. Vi skal ikkje rekne med imaginære tal i 1T-kurset, men bruk gjerne Internett og finn ut meir om imaginære og komplekse tal! (Komplekse tal er tal som inneheld ein reel del og ein imaginær del.)
Når vi skal referere til bestemte tal på tallinja, bruker vi klammeparentesar . Mengda av dei naturlege tala 1, 2 og 5 skriv vi som .
Mengda av alle reelle tal avgrensa av to verdiar kallar vi eit talintervall. Døme på talintervall er
og
Det første intervallet inkluderer tala 1 og 3 i tillegg til alle reelle tal mellom desse to tala.
Dette er eit lukka intervall.
I det andre intervallet er 1 og 3 ikkje med, men elles er alle tala som er med i det første intervallet også med her. Dette er eit ope intervall.
I det tredje intervallet er talet 1 ikkje med, medan talet 3 er med. I det fjerde er talet 1 med, medan 3 ikkje er med. Dei to siste intervalla kallar vi halvopne intervall.
Intervallet inneheld alle reelle tal større enn eller lik .
Intervallet inneheld alle reelle tal mindre enn .
Forklar kva som er skilnaden på eit lukka, eit ope og eit halvope intervall.