Eit praktisk eksempel på ein tredjegradsfunksjon

Tenk deg at du skal lage ei eske utan lokk av ei kvadratisk papplate med sidelengder
60 cm. Du må då klippe bort eit kvadrat i kvart hjørne av papplata.
Du må altså klippe bort dei fire mørkeblå kvadrata på teikninga nedanfor. Dei lyseblå rektangla brettar du opp, og du får då ei eske med det lyse kvadratet i midten som botn.
Forma på eska avheng av kor store kvadrat du klipper bort. Vi kallar sidene i kvadrata du klipper bort for . Dersom er stor, vil eska få ein liten botn, men blir desto høgare. Dersom er liten, vil eska få stor botn, men ho vil bli låg.
Volumet av eska vil vere avhengig av . Det vil seie at volumet er ein funksjon av . Vi vil finne ein formel for denne funksjonen.
Botnen til eska blir eit kvadrat med sider . Det kan vi lese ut av teikninga. Arealet av botnen, det vi kallar grunnflata, blir då
Høgda på eska blir . Vi må multiplisere grunnflata med høgda for å få volumet, her kalla .
Volumet er altså ein polynomfunksjon av tredje grad. Vi ser også at må liggje mellom 0 cm og 30 cm for at vi skal få ei eske. Definisjonsmengda er då
Dersom , klipper vi ikkje bort noko, og dersom , så får vi ikkje nokon botn.
Vi teiknar grafen av volumfunksjonen.
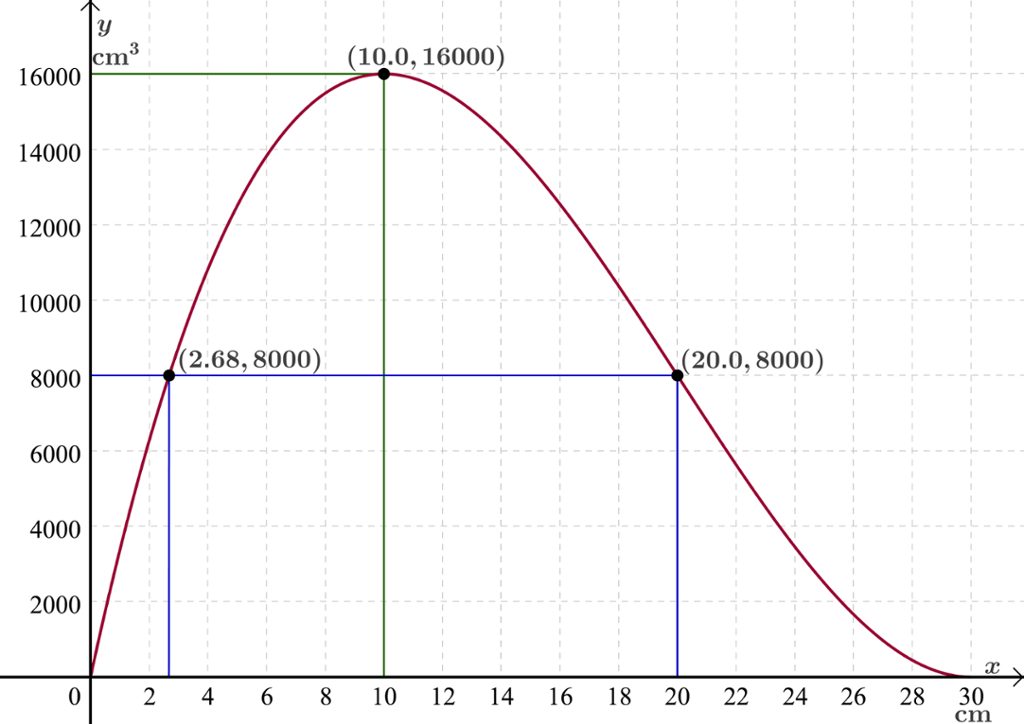
Vi ser av grafen at verdimengda er
Det vil seie at volumet til eska er større enn og mindre enn eller lik .
Vi kan elles sjå av grafen at
- dersom vi ønskjer ei eske med størst mogleg volum, må vi klippe bort kvadrat med sider
- dersom vi ønskjer ei eske med volum lik , må vi klippe bort kvadrat med sider eller
- vi òg kan gå motsett veg og lese av kor stort volum ein bestemd verdi av gir