Avstand punkt–linje. Vektorfunksjonar
Med avstanden frå eit punkt til ei rett linje
Prøv sjølv
Du kan dra i punktet
Kor stor er vinkelen mellom linja og linjestykket
Vi skal her vise to metodar for å finne denne avstanden. Det er viktig at du lærer deg begge metodane fordi dette er generelle metodar som kan brukast på andre problemstillingar.
Vi skal bruke ein trekant slik som på figuren til hjelp.
Tenk over
Korleis kan ein slik trekant hjelpe oss med å finne avstanden frå eit punkt til ei linje?
Vi set opp to ulike måtar for å finne arealet av ein trekant slik at vi får ei likning der vi kan bestemme
Vi kan rekne ut arealet ved hjelp av den vanlege arealformelen for trekantar:
A △ = 1 2 g · h = 1 2 a → · h Vi kan bruke arealformelen som inneheld vektorproduktet mellom
a → b → A △ = 1 2 a → × b →
Desse to formlane må gi det same arealet. Vi får
Døme
Vi har gitt punkta
Løysing utan hjelpemiddel
Vi byrjar med å finne
Vi får
Avstanden frå
Løysing med hjelpemiddel
Med CAS går dette raskare:
Kontroller at dette er det same svaret som vi fekk utan hjelpemiddel.
Er det vanskeleg å hugse formelen for avstanden
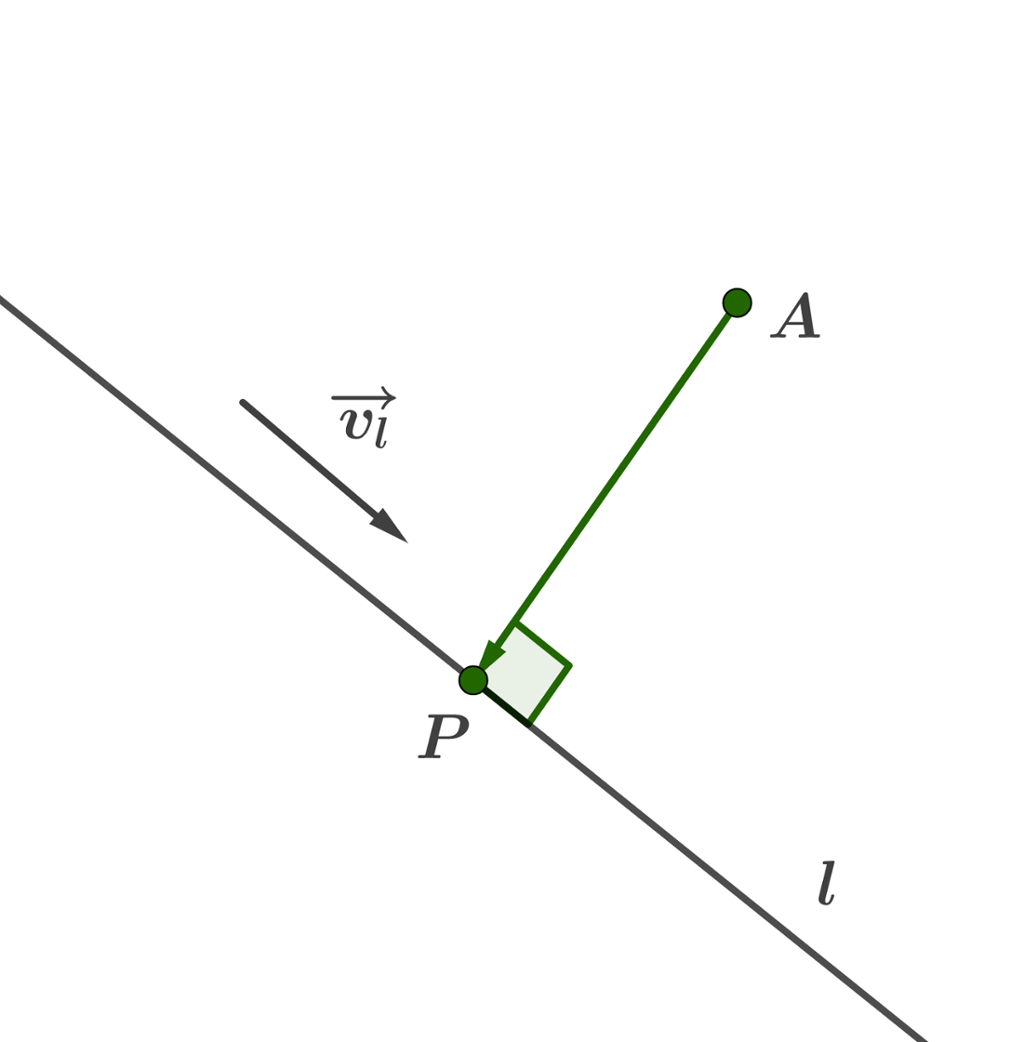
I den andre metoden bruker vi denne framgangsmåten:
- Vi finn eit uttrykk for vektoren frå punktet
A P ( x , y , z ) l - Vi finn deretter den verdien av parameteren som gjer at denne vektoren står vinkelrett på
l A P → · v → l = 0 v → l
retningsvektor for linjal Lengda av den vektoren vi då får, er avstanden frå
A l
Vi vel å vise framgangsmåten med eit døme.
Døme
Gitt ei linje på parameterform
Finn avstanden frå punktet
Løysing utan hjelpemiddel
Eit vilkårleg punkt
Vidare får vi at
For at lengda av
Dette gir vidare
Vi set denne
Avstanden frå
Avstanden frå punktet
Løysing med hjelpemiddel
Legg merke til i framgangsmåten med CAS nedanfor at vi skriv inn linja r(t). Vi gjer tilsvarande med AP(t). Dette er nødvendig for å kunne rekne med uttrykka på ein enkel måte.
Vi kan òg finne ein retningsvektor r(t). (Sjå forklaring lenger ned.)

I linje 4 finn vi ein retningsvektor vl for linja ved å derivere r(t). Vi ser at vi får same retningsvektor som vi brukte då vi løyste oppgåva utan hjelpemiddel over. I linje 5 løyser vi likninga AP(t).
Tenk over
Kvifor får vi ein retningsvektor for linja r(t)?
Når vi skriv linja r(t):=(4-t,5t,2-t) slik vi har gjort det i linje 1 i CAS-biletet over, kallar vi r(t) for ein vektorfunksjon. Vi ser på vektoren som ein funksjon av variabelen
Tenk over
Er AP(t) i linje 3 ein vektorfunksjon?
Vektorfunksjonar og kurver
Når vi skal rekne med linjer og kurver i CAS i GeoGebra som i dømet her, bør vi skrive dei inn som vektorfunksjonar slik vi har gjort. Dersom vi berre ønsker å teikne ei kurve, eller delar av ho, bruker vi kommandoen "Kurve".
I dømet i metode 1 (arealmetoden) hadde vi gitt tre punkt. Då er det som regel enklast å bruke denne metoden. I dømet i metode 2 (skalarproduktmetoden) der vi har gitt parameterframstillinga av linja, er det som regel enklast å bruke metode 2.