Tal og talmengder
Dei første tala du lærte som barn var sannsynlegvis tala
Dette var også dei første tala menneska tok i bruk.
Vi kallar desse tala for dei naturlege tala. Mengda av alle dei naturlege tala symboliserer vi med bokstaven .
Vi skriv
og les «N er lik mengda av tala osb». Vi bruker mengdeparentesar for å liste opp ei mengd av enkelttal. Prikkane etter 10-talet viser at tala held fram i same mønster, osb.
Dei naturlege tala kan brukast til å beskrive talet på noko, til dømes kor mange eple du har. Dei kan også brukast til å gi ei nummerrekkjefølgje , til dømes resultatlista ved ein idrettskonkurranse.
Den tyske matematikaren Leopold Kronecker skal ein gong ha sagt at «Gud skapte dei naturlege tala, resten er menneskeverk».

La oss tenkje oss at du dyrkar og sel eple. Dersom du har eple og sel eple, har du eple igjen. Dette kan illustrerast med rekneoperasjonen subtraksjon.
Vi subtraherer eit naturleg tal frå eit anna naturleg tal og får eit nytt naturleg tal.
Men kva dersom kunden ønskjer å kjøpe eple, eller til og med eple slik at du må låne 4 eple av naboen?
Reknestykka blir no
Her har vi ikkje naturlege tal som gir svar på rekneoperasjonane. Det er då matematikarar har funne på å utvide talmengda med talet og dei negative tala, og vi får at
Null eple tyder at du ikkje har fleire eple, og eple tyder at du skulder 4 eple.
Legg merke til at vi bruker minusteiknet som eit forteikn eller som eit rekneteikn!
Vi utvidar mengda av dei naturlege tala ved å plassere null til venstre til venstre for til venstre for og så vidare.
Tallet kan med fordel lesast som «negativ » for å markere at her bruker vi minusteiknet som eit forteikn, det fortel at talet er negativt, og ikkje som rekneteiknet subtraksjon.
Den talmengda vi no har fått kallar vi for heile tal og symboliserer ho med .
Når vi bruker rekneoperasjonane addisjon og subtraksjon på to heile tal, får vi alltid eit nytt heilt tal som resultat.
Ei tallinje kan gi eit bilde av dei heile tala
Tal som ligg på kvar si side av talet , og like langt frå , blir kalla motsette tal. Til dømes er og motsette av kvarandre. Summen av eit tal og det motsette talet er alltid lik null. Talet er sitt eige motsette tal.
Motsette tal: og
Dei negative tala vart ikkje førte inn i Europa før på -talet. Det var store diskusjonar før dei vart godtatt. Både filosofar og teologar var sterkt i tvil til å godta negative tal.
Talet vart godtatt i Europa nokre hundre år tidlegare. Nokre matematikarar reknar talet med blant dei naturlege tala, medan andre ikkje gjer det. (Det er faktisk ingen som er gitt myndigheit til å bestemme til dømes om talet skal reknast som eit naturleg tal eller ikkje!)
Når vi legg saman, trekkjer frå kvarandre og multipliserer heile tal, blir resultatet alltid eit heilt tal. Det er slik ein matematikar likar å ha det. Éi talmengd og éin rekneoperasjon! Rekneoperasjonen verkar på tal i talmengda og gir eit nytt tal i talmengda.
Når vi adderer eit positivt tal, flyttar vi oss til høgre på tallinja. Adderer vi det positive talet , flyttar vi oss to plassar til høgre på tallinja, anten vi adderer talet til eit positivt eller negativt tal.
Når vi subtraherer eit positivt tal, flyttar vi oss til venstre på tallinja. Subtraherer vi det positive talet , flyttar vi oss to plassar til venstre på tallinja. Dersom vi subtraherer det positive talet , flyttar vi oss ni plassar til venstre på tallinja.
Men kva vil det seie å addere eller subtrahere negative tal?
Kor hamnar vi på tallinja dersom vi til talet adderer det negative talet , eller til talet subtraherer det negative talet ?
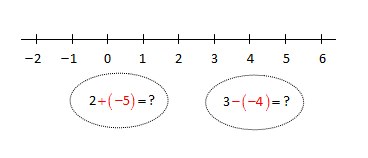
Kva vil det eigentleg seie å addere og subtrahere negative tal? Har vi praktiske situasjonar der vi kan få ei forståing av kva det vil seie? Dette kjem vi tilbake til i Å rekne med negative tal!