Regresjon og modellering

Å gjere ein lineær regresjon betyr å gå frå observerte/gitte data til ein lineær modell som kan brukast til å beskrive dataa. Ein slik modell kan vi òg bruke til å seie noko om omtrentlege verdiar utanom dei observerte dataa våre. I denne artikkelen skal vi ta utgangspunkt i to døme for å vise korleis vi kan gjere ein regresjon. Vi gjer den eine regresjonen med GeoGebra og den andre med Python.

Folketalsutvikling i Noreg – regresjon med GeoGebra

Tabellen under er henta frå statistisk sentralbyrå (SSB) og viser folketalet i Noreg for nokre utvalde år i perioden frå 1950 til 2000.

Vi ønsker å undersøke om det er ein samanheng mellom årstal etter 1950 og folketalet.
Når vi skal lage modellar der vi ser på utvikling over tid, er det vanleg å bruke andre verdiar enn årstala på x-aksen. Det kan òg vere lurt å ikkje ha for store eller små tal på aksane. Vi har derfor laga ein ny tabell der x er talet på år etter 1950 og $f\left(x\right)$ er folketalet i millionar:

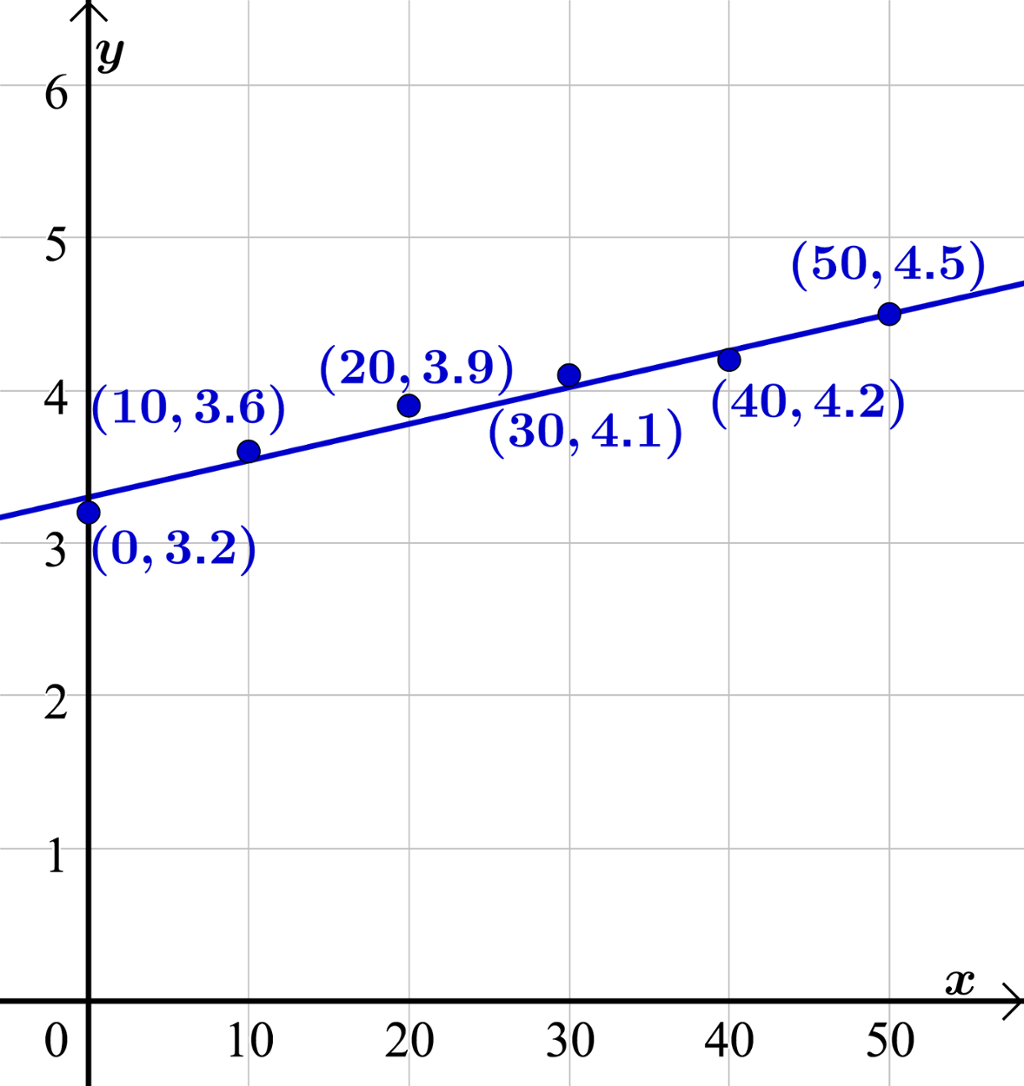
Vi plottar punkta i eit koordinatsystem for å sjå om det er ein samanheng mellom talet på år som har gått sidan 1950, og kor mange innbyggarar det er i Noreg.

Vi ser at punkta ligg tilnærma på ei rett linje. Dette betyr at folketalet i Noreg har hatt ein tilnærma lineær vekst i perioden frå 1950 til 2000.

Vi ønsker å finne likninga til den linja som best tilnærmar denne veksten.

Vi vel "Rekneark" i GeoGebra og legg tala frå tabellen inn i reknearket. Legg merke til at det lønner seg å legge x-verdiane og y-verdiane i kvar sin kolonne. Merk så området der du har lagt tala, vel "Regresjonsanalyse". Vel lineær modell i nedtrekksmenyen. Du får då opp dette biletet:

Vi har at funksjonen $$ f\left(x\right)=0,0243x+3,3095$$ er ein matematisk modell som tilnærma beskriv utviklinga i Noreg frå 1950 til 2000.

Stigningstalet er 0,024 3. Det betyr at etter denne modellen aukar folketalet i Noreg gjennomsnittleg med 24 300 personar per år, og folketalet vil vere 4,87 millionar i år 2015. Sjå punktet (65, 4.87) på grafen nedanfor.

Tal frå SSB viser at folketalet i Noreg var 4,6 millionar i 2005 og 4,9 millionar i 2010. Det passerte 5,2 millionar i 2015. Sjå punkta i diagrammet. Folketilvekst i 2014 var ifølge SSB på 56 749 personar.

🤔 Tenk over: Synest du modellen frå år 2000 var ein god modell til å føreseie folketalsutviklinga i åra 2000 til 2015? Undersøk kva folketalet i Noreg er i dag. Meiner du at modellen frå år 2000 framleis kan brukast til å føreseie framtidig folketalsutvikling, eller bør det lagast nye modellar?

Overføring av modellen til grafikkfeltet

Dersom du skal arbeide vidare med modellen du har laga, kan du overføre modellen til grafikkfeltet ved hjelp av knappen ved sidan av "punktdiagram" og velje "Kopier til grafikkfeltet".

Omkrins av ein sirkel – regresjon med Python

Vi vil undersøke samanhengen mellom radius til ein sirkel og omkrinsen av sirkelen.

Vi har valt å bruke GeoGebra til å teikne fire sirklar med radius på høvesvis 0,31 cm, 1,40 cm, 2,30 cm og 3,30 cm.

Deretter har vi brukt kommandoen "Omkrins()" i algebrafeltet for å finne omkrinsen til sirklane, som vist på biletet.

For kvar verdi av radius, som vi kan kalle x, får vi ein verdi for omkrinsen, som vi kan kalle $g\left(x\right)$. Vi seier at omkrinsen er ein funksjon av radius, x.

Vi set resultata opp i ein tabell.

Vi gjer som i dømet over: Vi må først sjekke om punkta ser ut til å vise ein samanheng mellom radius og omkrins. Til det bruker vi funksjonen "scatter()". Programmet kan sjå slik ut:

1import matplotlib.pyplot as plt
2
3X = [0.31, 1.40,2.30,3.30]
4Y = [1.95,8.80,14.45,20.73]
5
6plt.scatter(X,Y)
7
8plt.show()

Køyr koden, og du vil oppdage at punkta ser ut til å ligge på ei rett linje.

For å finne den rette linja i Python importerer vi "curve_fit" frå biblioteket "scipy.optimize". Programmet for å gjere ein lineær regresjon og teikne målepunkta og modellen kan sjå slik ut:

1import matplotlib.pyplot as plt
2from scipy.optimize import curve_fit
3import numpy as np
4
5def modell(x,a,b):
6    return a*x + b
7
8X = [0.31, 1.40,2.30,3.30]
9Y = [1.95,8.80,14.45,20.73]
10
11konstantar, kovarians = curve_fit(modell, X,Y)
12
13a,b = konstantar
14
15print(f'f(x)= {a:.2f}x+{b:.3f}')
16
17#teiknar modellen vi fann, saman med punkta
18
19X_2 = np.array(X)
20Y_2 = modell(X_2,a,b)
21
22plt.plot(X_2,Y_2)    #teiknar modellen
23
24plt.scatter(X,Y)     #teiknar målepunkta
25
26plt.show()

Når vi køyrer denne koden, får vi modellen $$ f\left(x\right)=6,28x + 0,005$$.

🤔 Tenk over: Du har tidlegare lært at omkrinsen til ein sirkel er $$ O=2\pi r$$. Korleis stemmer eigentleg det med funksjonen du fann?

I kompetansemåla står det at du skal kunne vurdere kor gyldig ein modell er.

Formelen for samanhengen mellom radius i ein sirkel og omkrinsen av sirkelen, $$ O=2\pi r$$, er eit døme på ein matematisk modell som er svært nøyaktig. Det har blitt gjort mange målingar som viser at vi kan stole på modellen. Den modellen vi fann ved hjelp av Python, var mindre nøyaktig fordi vi ikkje hadde heilt nøyaktige måltal. Likevel vil modellen vår òg vere nokså nøyaktig for store verdiar av x.

Modellen vi fann for å beskrive korleis folketalet i Noreg utviklar seg, er meir usikker. For det første ser vi at linja ikkje treffer punkta frå tabellen heilt nøyaktig. Den linja som kjem fram ved lineær regresjon, er den som totalt sett har minst avvik frå punkta.

Den lineære modellen har stigningstal 0,024 3. Det betyr ein vekst i folketalet på 0,024 3 millionar eller 24 300 per år. Er det realistisk at folketalet her i landet vil auke med cirka 25 000 per år i tida framover?

Kor lenge vil denne utviklinga i så fall halde fram? Det er ikkje lett å svare på dette. Her er det mange faktorar som kan verke inn. Vil politikarane avgrense innvandringa til Noreg, eller vil dei opne for fri innvandring? Kva med fødselspermisjonar og barnehagetilbod? Vil det bli lettare eller vanskelegare å vere småbarnsforeldre?

Vi kan stille liknande spørsmål til andre matematiske modellar. Vi må alltid vurdere om ein matematisk modell er gyldig, og spesielt må vi ta omsyn til forhold som kan påverke situasjonen før vi bruker ein modell til å seie noko om kva som vil skje i framtida.

Nedanfor kan du teste kodane dine dersom du ikkje har ein eigen editor tilgjengeleg. NB: Editoren vil ikkje vere tilgjengeleg under skriftleg eksamen.