Modell for utgifter til leie av selskapslokale
To firma leiger ut selskapslokale.
Firma A tek ein fast leigepris på kroner og eit timetillegg på kroner. Kostnadene i kroner, , ved leige av lokalet i timar kan beskrivast med funksjonsuttrykket eller modellen
Firma B tek ein fast leigepris på kroner og eit timetillegg på kroner. Kostnadene i kroner, , ved leige av lokalet i timar kan beskrivast med funksjonsuttrykket eller modellen
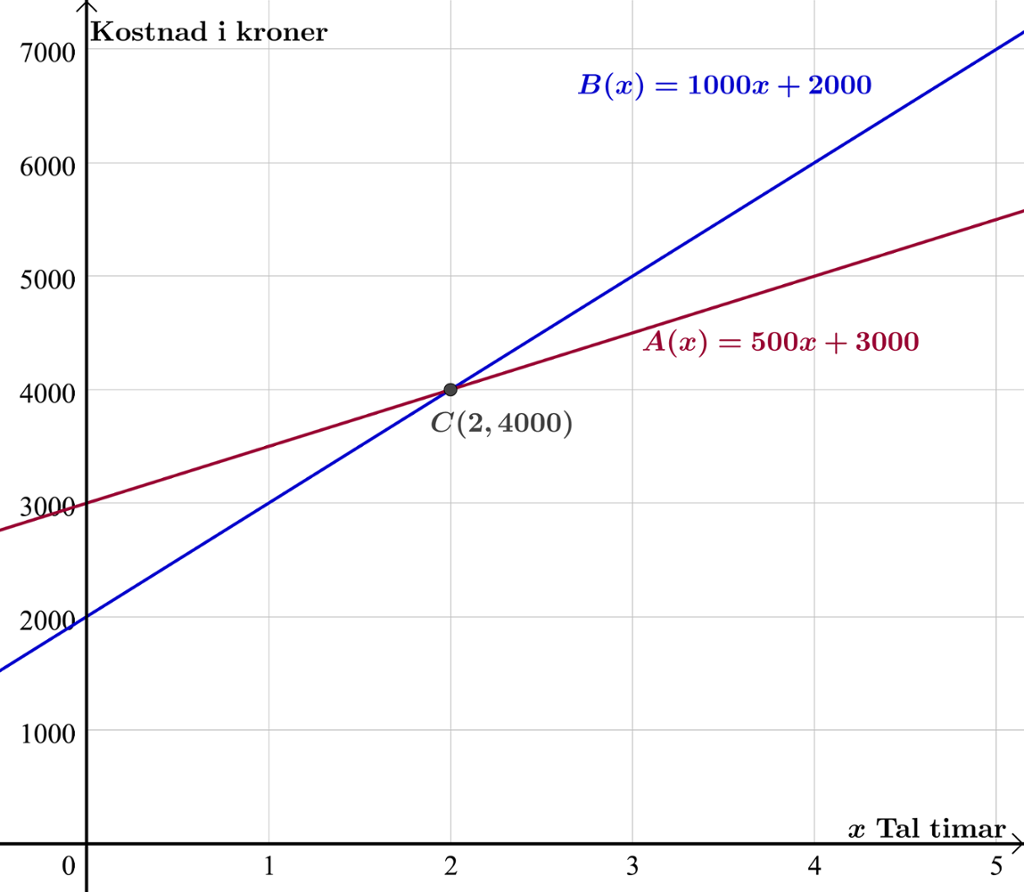
Vi teiknar grafane til dei to funksjonane og finn skjeringspunktet mellom grafane ved kommandoen «Skjering mellom to objekt».
Grafane skjer kvarandre når . Det betyr at om du skal leige lokala i to timar, er det prismessig det same kva firma du vel. Prisen er kroner hos begge firmaa.
Om du skal leige lokalet i mindre enn to timar, løner det seg å velje firma B. Det ser vi ved at grafen til ligg under grafen til i dette området.
Om du skal leige lokalet i meir enn to timar, løner det seg å velje firma A. Det ser vi ved at grafen til ligg under grafen til i dette området.

Vi kan kontrollere den grafiske løysinga ved rekning.
Vi får òg her at leigeprisane er like når leigetida er to timar og at leigeprisen då er kroner.
Hos firma A er totalkostnadene i kroner ved leige av lokalet i timar gitt ved funksjonsuttrykket
Konstantleddet er og viser her at den faste leigeprisen er kroner . Han må betalast same kor mange timar lokalet blir leigt. Legg merke til at grafen skjer -aksen i punktet .
Stigingstalet er . Det betyr at det kostar kroner for kvar ekstra time lokalet blir leigt.
Kostnadene aukar jamt med auken i talet på leigde timar. Vi har lineær vekst i kostnadene.
Funksjonen gitt ved gir strekninga i meter som er sprungne etter minutt.
Her er konstantleddet lik null, og det viser at sprungen strekning er null ved tida null. «Klokka» startar når løpeturen byrjar.
Stigingstalet er . Det betyr det blir sprunge meter for kvart ekstra minutt. Det fortel altså at farten er meter per minutt.
Talet på sprungne meter aukar jamt med auken i talet på minutt det blir sprunge. Vi har lineær vekst i talet på sprungne meter.