Forsøk
Modell for svingetida til ein pendel
Kva skjer med svingetida til ein pendel dersom vi endrar snorlengda?
Bilete: Stein Aanensen, Olav Kristensen / CC BY-NC-SA 4.0
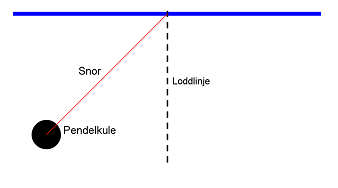
På figuren til høgre ser du ei skisse av ein pendel. Når du dreg pendelkula ut til sida slik figuren viser, og slepper henne, vil ho svinge fram og tilbake.
Svingetida til pendelen er tida det tek frå du slepper pendelkula, til ho er tilbake i same posisjon. Svingetida måler vi i sekund.
Svingetida endrar seg når vi endrar lengda på snora. Vi ønskjer å finne samanhengen mellom snorlengd og svingetid.

Heimelaga pendel. Bilete: NTB scanpix, Science Photo Library / CC BY-NC-SA 4.0
Praktisk oppgåve
Gå saman i små grupper. Finn ein eigna plass til å hengje opp ein pendel. For at luftmotstanden ikkje skal forstyrre målingane, bør de bruke eit relativt tungt lodd som pendelkule og la pendelsnora vere så tynn som mogleg. Hugs at vi måler snorlengda frå opphengingspunktet til midt i pendelkula..
- Mål svingetida for pendelen ved ulike snorlengder. La snorlengda variere frå 0 til 4 meter.
- Legg resultata inn i ein tabell i reknearket i GeoGebra.
- Merk tabellen, vel «Regresjonsanalyse» og deretter «Analyser».
- Vel etter tur dei ulike funksjonstypane og kopier dei til grafikkfeltet. Finn den kurva som passar best med punkta i grafikkvindauget.
- Kva for ein modell for svingetida til pendelen passar best?
- Vis korleis du kan bruke modellen til å rekne ut svingetida når du kjenner snorlengda.