Fagartikkel

Lineære funksjonar

Lineære funksjonar er funksjonar som beskriv rette linjer. Den generelle likninga for ei rett linje er y = ax + b.

Den generelle lineære funksjonen

Ein lineær funksjon er ein funksjon der den uavhengige variabelen x berre finst i første potens. Dersom vi teiknar grafen til funksjonen, får vi ei rett linje.

Definisjon

Ein funksjon som kan skrivast på forma

$f (x) = a x + b$

der koeffisientane $a, b \in ℝ$ , kallar vi ein lineær funksjon eller ein førstegradsfunksjon. Grafen til ein førstegradsfunksjon blir ei rett linje.

Stigningstal og konstantledd

Før du les vidare, kan det vere lurt å gjere oppgåve 1 på oppgåvesida om lineære funksjonar. Der kan du utforske kva endringar av koeffisientane a og b gjer med grafen til funksjonen.

Koordinatsystem med x-verdiar frå minus 2 til 3 og y-verdiar frå minus 4 til 1. Grafen til f av x er lik 2 x minus 2 er teikna inn. Han er ei rett linje. Grafen skjer andreaksen for y er lik minus 2 og x-aksen for x er lik 1. Stigningstalet a er lik 2 og punktet 0 og minus 2 er også teikna inn. Illustrasjon.

På biletet har vi teikna grafen til $f (x)$ for $a = 2$ og $b = - 2$ . Det betyr at $f (x) = 2 x - 2$ .

Legg du merke til at grafen skjer y-aksen der $y = - 2$ ? Grafen skjer andreaksen når $x = 0$ og
$y = f (0) = a \cdot 0 + b = b$ , det vil seie i punktet $(0, b)$ .

Koeffisienten b kallar vi konstantleddet.

a viser kor mykje grafen stig når x aukar med 1 eining.

Koeffisienten a kallar vi stigningstalet.

Dersom stigningstalet er negativt, søkk grafen når x aukar.

Meir om stigningstalet

I eit koordinatsystem der x-aksen går frå 0 til 4 og y-aksen går frå 0 til 5,5 er det teikna ei rett linje. Linja går gjennom punktet med koordinatane 1 og 1 og punktet med koordinatane 3 og 5. Det er teikna ei pil frå det første punktet med koordinatane 1 og 1 til punktet med koordinatane 3 og 1. Pila har tilhøyrande tekst 2 til høgre. Frå punktet med koordinatane 3 og 1 er det teikna ei pil til punktet med koordinatane 3 og 5 på linja. Pila har tilhøyrande tekst 4 opp. Illustrasjon.

I avsnittet over ser vi at vi kan lese av stigningstalet ved å starte i eit punkt på grafen, gå éi eining til høgre på x-aksen og så lese av kor langt opp eller ned vi må gå for å treffe på grafen. Av og til kan det derimot vere vanskeleg å lese nøyaktig av ved å berre gå nøyaktig éi eining til høgre. Det kan derfor vere nyttig å ha fleire strategiar for å finne stigningstalet. Vi ser på eit nytt døme.

Ved å starte i til dømes punktet (1, 1) og gå to einingar til høgre, må vi gå fire einingar oppover parallelt med y-aksen for igjen å treffe grafen. Stigningstalet blir

$a = \frac{4}{2} = 2$

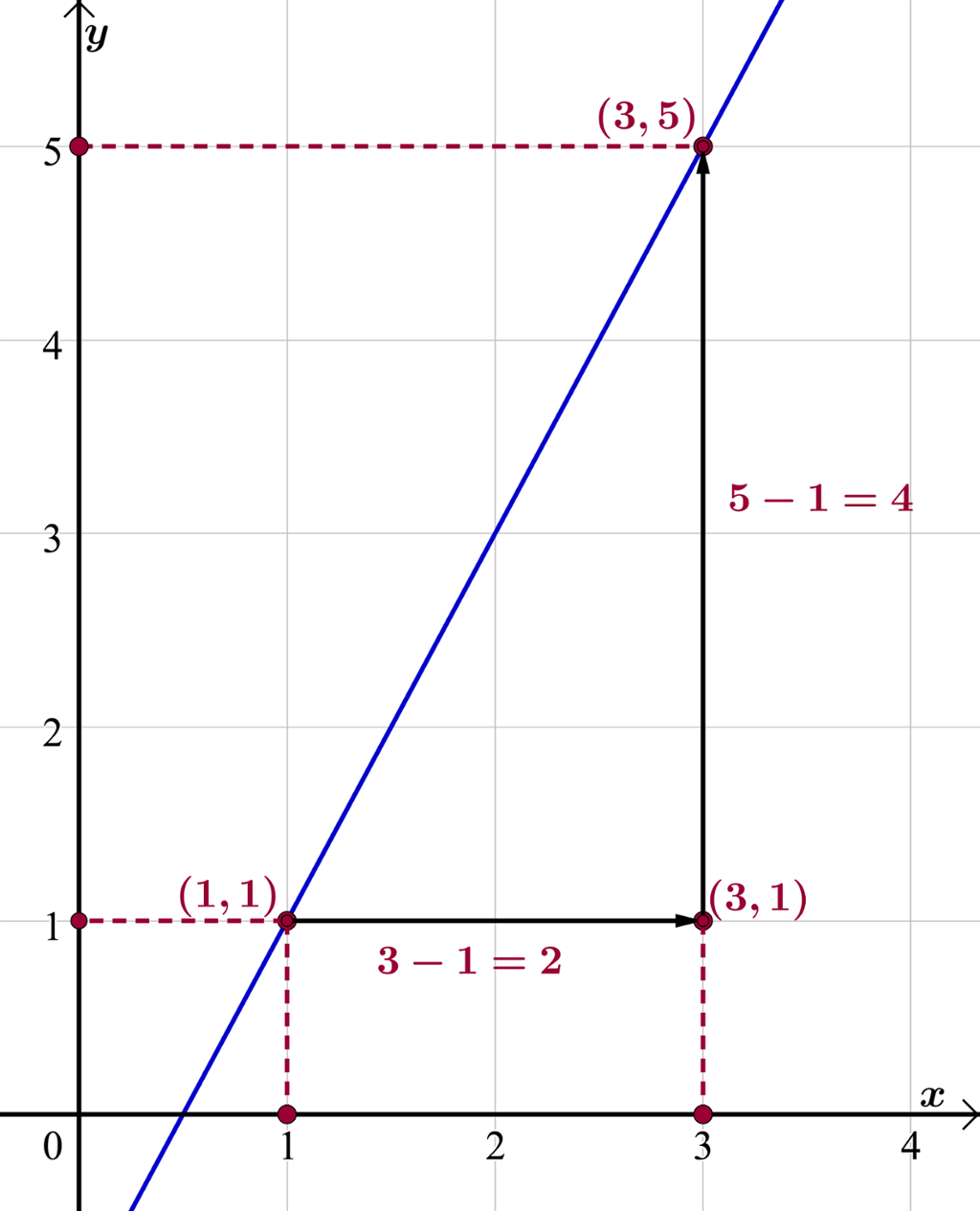
Dette kan vi òg rekne oss fram til med utgangspunkt i koordinatane til dei to punkta på grafen

$a = \frac{5 - 1}{3 - 1} = \frac{4}{2} = 2$

I teljaren har vi endring i y-verdi, og i nemnaren har vi endring i x-verdi.

Endring i y-verdi dividert med endring i x-verdi gir alltid verdien for stigningstalet fordi stigningstalet er endring i y-retning per eining på x-aksen.

Generell formel for stigningstalet

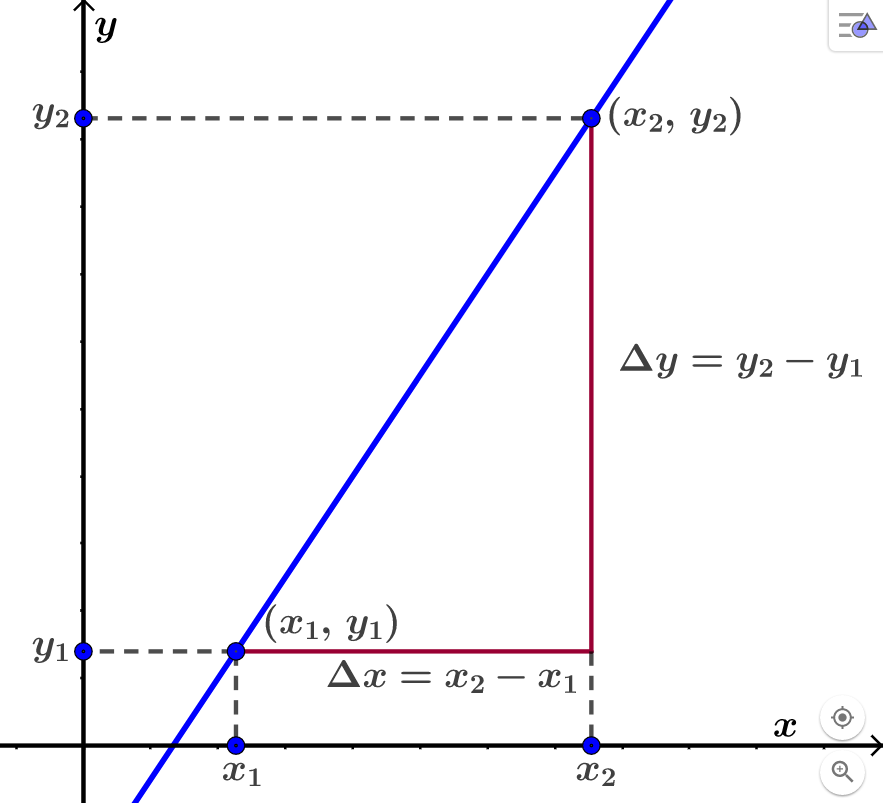
I eit koordinatsystem utan tal på aksane er det teikna ei rett linje. Linja går gjennom punktet med koordinatane x 1 og y 1 og punktet med koordinatane x 2 og y 2. Det er teikna eit vassrett linjestykke frå det første punktet med koordinatane x 1 og y 1 til punktet med koordinatane x 2 og y 1. Linjestykket har tilhøyrande tekst delta x er lik x 2 minus x 1. Frå punktet med koordinatane x 2 og y 1 er det teikna eit loddrett linjestykke til punktet med koordinatane x 2 og y 2 på den opphavlege linja. Linjestykket har tilhøyrande tekst delta y er lik y 2 minus y 1. Illustrasjon.

Vi lar no $(x_{1}, y_{1})$ og $(x_{2}, y_{2})$ vere to vilkårlege punkt på linja. Legg merke til korleis vi bruker indeksar, 1 og 2, for å "namngi" punkt 1 og punkt 2.

Det er vanleg å la den greske bokstaven delta, $Δ$ , stå for endring.

Vi lar $Δ x = x_{2} - x_{1}$ vere endring i x-verdi og $Δ y = y_{2} - y_{1}$ vere endring i y-verdi.

Dette gir oss denne formelen:

Generell formel for stigningstalet til ei rett linje

$a = \frac{y_{2} - y_{1}}{x_{2} - x_{1}} = \frac{Δ y}{Δ x}$

To spesialtilfelle

Du bør merke deg to spesialtilfelle av lineære funksjonar.

Det eine er når $b = 0$ . Da er $f (x) = a x$ , og y og x er proporsjonale storleikar. Talet a kallar vi i dette tilfellet proporsjonalitetskonstanten.

Det andre spesialtilfellet er når $a = 0$ . Da er $f (x) = b$ , og grafen er parallell med x-aksen.

Å teikne grafen til ein lineær funksjon

Vi skal sjå på korleis vi kan teikne grafen til ein lineær funksjon for hand. Vi tek utgangspunkt i funksjonen $f (x) = - 2 x + 4$ og viser to ulike metodar.

Vi bruker verditabell

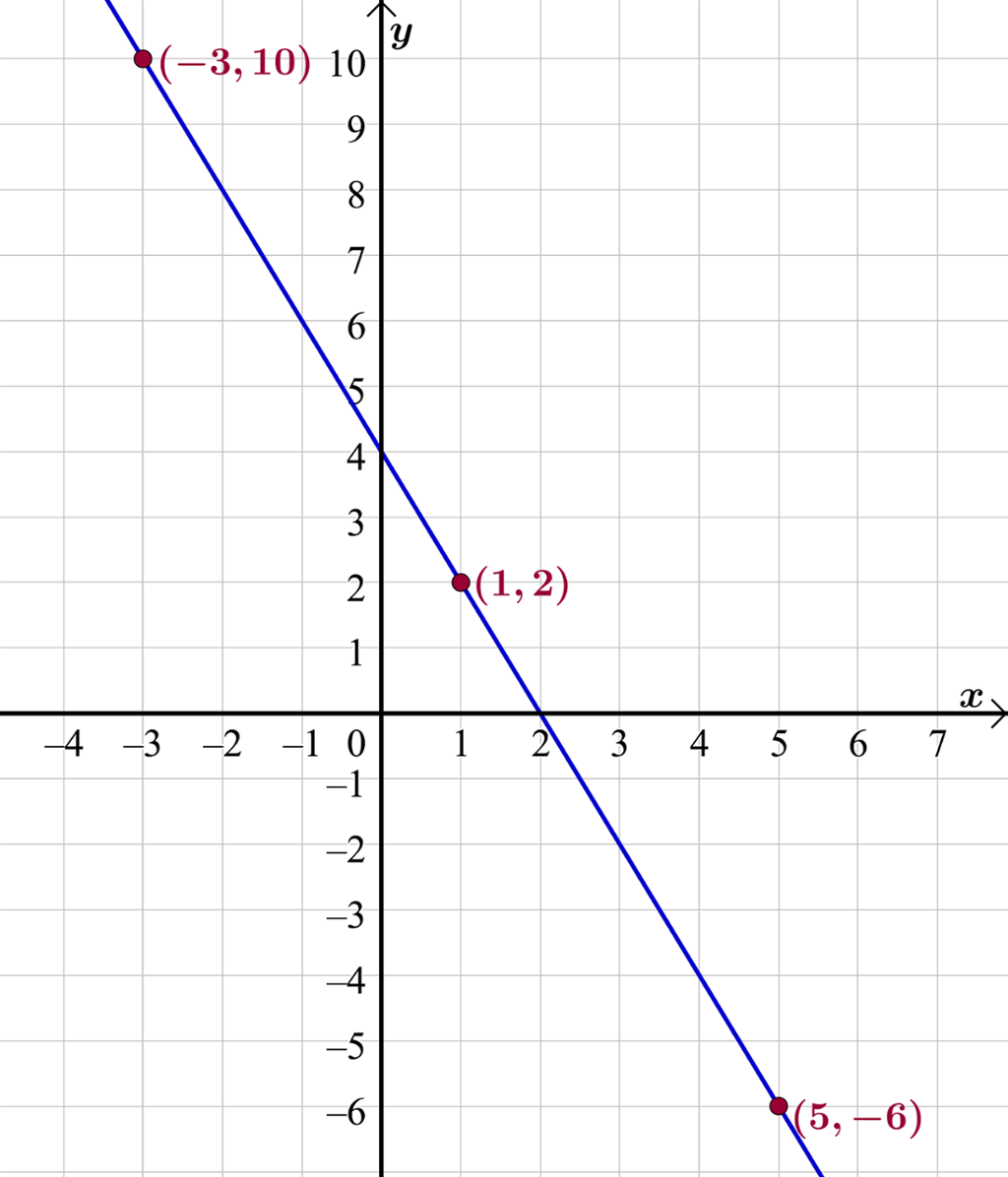
Grafen til ein lineær funksjon gjennom punktet med koordinatane minus 3 og 10, punktet med koordinatane 1 og 2 og punktet med koordinatane 5 og minus 6 er teikna i eit koordinatsystem. Illustrasjon.

Vi veit at grafen blir ei rett linje. Då er det eigentleg nok med to punkt i verditabellen sidan ei rett linje er eintydig bestemd av to punkt på linja. Det er likevel lurt å ta med eit tredje punkt som kontroll. Dersom alle dei tre punkta ligg på ei rett linje, veit vi at vi har rekna rett.

Vi fyller ut tabellen. Etterpå kan vi teikne inn punkta og trekke linja som går gjennom dei slik som på biletet:

Verditabell
x	f(x)
-3	10
1	2
5	-6

Vi bruker konstantledd og stigningstal

Grafen til ein lineær funksjon som går gjennom punkta med koordinatar 0 og 4 og 1 og 2 er teikna i eit koordinatsystem. Figuren viser at dersom ein går 1 eining til venstre frå punktet med koordinatar 0 og 4, må ein gå 2 einingar ned for å komme til grafen igjen. Illustrasjon.

Sidan konstantleddet $b = 4$ , skjer grafen andreaksen for $y = 4$ . Punktet (0, 4) ligg derfor på grafen.

Stigningstalet er $- 2$ . Vi tek utgangspunkt i punktet (0, 4), går ein eining til høgre, og stigningstalet fortel at vi må bevege oss parallelt med y-aksen 2 einingar ned for igjen å møte grafen. Vi kjem til punktet (1, 2). Vi har då to punkt på grafen og kan trekke linja gjennom desse punkta.

Samanfatning

Ein lineær funksjon er på forma $f (x) = a x + b$ .

a er stigningstalet og gir oss stigninga på linja.

b er konstantleddet og gir oss kryssingspunktet med y-aksen.

Generell formel for stigningstalet er

$a = \frac{Δ y}{Δ x}$